Минимизация функции

Минимизация (упрощение формы записи) функции являет­ся важной операцией при синтезе логической схемы, так как благода­ря предварительно проведенной минимизации схема реализуется с наименьшим числом элементов.

Выявить и устранить избыточность в записи функции можно путем ее преобразований с использованием аксиом, законов, тождеств и теорем алгебры логики. Однако такие преобразования требуют гро­моздких выкладок и связаны с большой затратой времени.

Современная алгебра логики располагает рядом приемов, разра­ботанных на основе ее правил, позволяющих производить минимиза-

цию функции более просто, быстро и безошибочно. Для минимизации функции с числом переменных до пяти-шести наиболее удобным яв­ляется метод карт Карно.

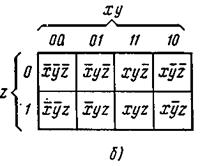
Карта Карно (рис. 3.20, а — б) представляет собой графическое изображение значений всех возможных комбинаций переменных. Иными словами, карту Карно можно рассматривать как графическое представление всех минтермов заданного числа переменных.

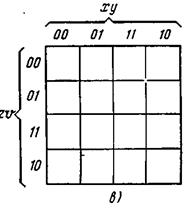
Рис. 3.20. Карта Карно функции для двух (а), трех (б) и четырех (в) переменных

Каждый минтерм изображается на карте в виде клетки. Карта образуется путем такого расположения клеток, при котором минтермы соседних клеток отличаются только значением одной пе­ременной. В связи с указанным соседними считаются также крайние клетки каждого столбца или строки. Символ «1» характеризует пря­мое значение переменной, а «0» — ее инверсное значение.

Минтермы минимизируемой функции отмечают единицами в соот­ветствующих клетках карты. Минтермы, не входящие в функцию, отмечают в клетках нулями или оставляют клетки пустыми. На осно­вании распределительного закона (3.58), а также аксиом 1 и 4 в (3.55) два минтерма, находящиеся в соседних клетках, могут быть заменены одним логическим произведением, содержащим на одну переменную меньше. Если соседними являются две пары минтермов, то такая группа из четырех минтермов может быть заменена произведением, содер­жащим уже на две переменные меньше, и т. д. В общем случае нали­чие единиц в 2ⁿ соседних клетках позволяет исключить п переменных. В этом и заключается метод минимизации с применением карт Карно.

Рассмотрим процесс минимизации на примере четырех переменных х, у, z, v функции, заданной следующим логическим выражением:

С помощью простейших преобразований представим эту функцию в виде

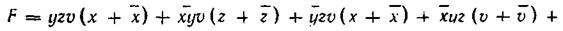
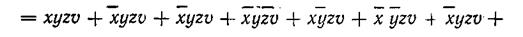
После исключения повторяющихся членов функция выражается в СДНФ:

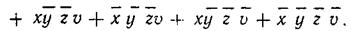
Функция состоит из 11 минтермов, в связи с чем на карте Карно (рис. 3.21) ее будут представлять 11 клеток, отмеченных единицами.

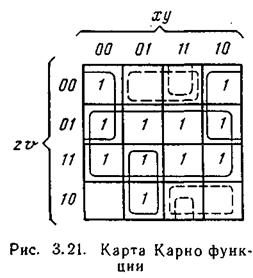
Так, например, первый минтерм функ­ции xyzv будет отображаться клеткой, имеющей координаты ху и zv, соответст­венно 11 и 11. Пять клеток карты ос­таются свободными.

Затем на карте Карно необходимо определить соседние минтермы (клетки) и объединить их в минимальное количе­ство групп соседних минтермов (клеток). Для наглядности выделенные группы соседних клеток показывают сплошны­ми линиями. Минимальное количество групп соседних минтермов для рассмат­риваемой функции будет равно трем.

В первую группу входят две нижние клетки второго столбца слева с мин-

термами `xyzv и `xyz` v. В соответствии с аксиомой 4 в (3.55) имеем

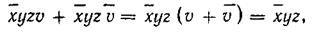
т. е. переменная vиз этой группы может быть исключена.

Вторая группа состоит из двух пар верхних клеток крайних столб-

цов, определяющих минтермы

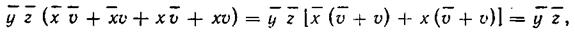
т. е. из группы исключаются две переменные: х и v.

Третья группа состоит из восьми клеток второй и третьей строк, для которых v — 1, а переменные х, у, z входят с прямыми и инверс­ными значениями, в связи с чем переменные х, у, г из этой группы мо­гут быть исключены. Сумма минтермов обеих строк будет равна v.

На основании проведенных операций получаем минимальную функцию, выраженную в ДНФ:

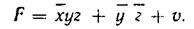
Карта Карно позволяет также провести минимизацию той же функ­ции в КНФ по нулевым значениям минтермов, находящихся в пустых клетках карты (рис. 3.21) и определяющих нулевое значение функции,

т. е. ее инверсное значение `F. Порядок проведения минимизации сохра­няется прежним. Минимизирующие контуры, охватывающие соседние клетки с нулевым значением минтермов рассматриваемой функции, показаны на рис. 3.21 пунктиром. Из карты Карно находим

Воспользовавшись инверсным преобразованием (3.61) находим минимальную функцию, выраженную в КНФ, равносильную ДНФ:

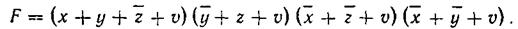
Минимизация функции в ДНФ или КНФ равноправна. Представ­ление результата минимизации в ДНФ или КНФ зависит от вида функции и состава используемых логических элементов. Реализация функции в ДНФ требует преимущественного использования логиче­ских элементов И (И — НЕ), а в КНФ — логических элементов ИЛИ (ИЛИ —НЕ) (см. §3.10).

При использовании логических элементов И (И — НЕ) логическую функцию целесообразно представить в виде произведения переменных, а логических элементов ИЛИ (ИЛИ — НЕ) — в виде суммы перемен­ных. Задачу решают, воспользовавшись правилом двойной инверсии и теоремой де Моргана. Для рассматриваемой функции соответственно имеем:

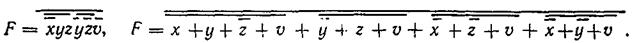
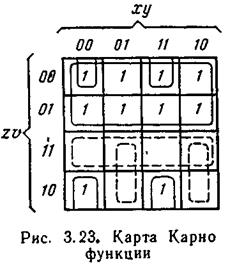
В качестве примеров определим минимальные функции в ДНФ и КНФ, представленные в виде карт Карно для трех переменных (рис. 3.22) и четырех переменных (рис. 3.23).

При нахождении минимальной функции в ДНФ, представленной картой Карно на рис. 3.22, группировочные контуры должны охваты­вать минтермы крайних столбцов 1 и 4 (первый контур) и минтермы

нижней строки (второй контур).

В первой группе минтермов результат не зависит от значений x и z, так как они могут принимать либо состояние «0», либо состояние

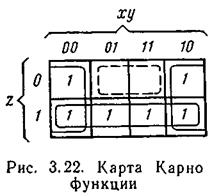
«1». Переменные х и z можно исключить. В итоге первое слагаемое оп­ределяемой минимальной функции равно `у. Во второй группе минтер­мов результат не зависит от значений х и y, следовательно, второе слагаемое определяется переменной г. Таким образом, имеем мини­мальную функцию в ДНФ:

или

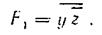
Минимальную функцию в КНФ находят из группировки двух пус­тых клеток карты:

откуда

т. е. дизъюнктивная и конъюнктивная минимальные формы рассмот­ренной функции совпадают.

Для получения минимальной функции в ДНФ, представленной кар­той Карно на рис. 3.23, необходимо составить три минимизирующих контура. В первый контур входят нижняя и верхняя клетки крайне­го левого столбца, откуда находим первое слагаемое минимальной

функции `х`y`v. Второй контур состоит из верхней и нижней клеток вто­рого столбца справа, откуда определяем второе слагаемое x y`v. И, на­конец, третий контур охватывает две верхние строки карты с резуль­татом г. Таким образом, получаем минимальную функцию в ДНФ:

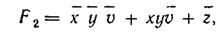
или

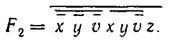
Минимальную функцию в КНФ находят из трех контуров, охва­тывающих пустые клетки:

с прямым значением

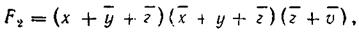
или

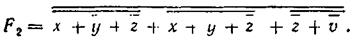
Нахождение логических функций и последущую их минимизацию широко применяют при проектировании логических схем комбина­ционного типа (см. § 3.15).

§3.10. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА ДИОДАХ И БИПОЛЯРНЫХ ТРАНЗИСТОРАХ

Логические элементы (узлы) предназначены для выполнения различных логических (функциональ­ных) операций над дискретными сигналами при двоичном способе их представления.

Преимущественное распространение получили логические эле­менты потенциального типа. В них используются дискрет­ные сигналы, нулевому значению которых соответствует уровень низкого потенциала, а единичному значению — уровень высокого по­тенциала (отрицательного или положительного). Связь потенциаль­ного логического элемента с предыдущим и последующими узлами в системе осуществляется непосредственно, без при­менения реактивных компонентов. Благодаря этому преимуществу именно потенциальные логические элементы наш­ли почти исключительное применение в интегральном исполнении в виде микросхем. С позиций использования логических микросхем потенциального типа и проводится далее рассмотрение логических элементов.

Логические биполярные микросхемы чаще выполняют на тран­зисторах типа п-р-п с напряжением питания Е_к> 0. Этим объясняет­ся, что используемые здесь сигналы имеют положительную поляр­ность. Уровню высокого положительного потенциала («1») на выходе соответствует закрытое состояние транзистора, а уровню низкого потенциала («О») — его открытое состояние. С этой точки зрения, в частности, и следует понимать действие сигнала на входе логического элемента, имеющего непосредственную связь в другими элементами в конкретной схеме. Для упрощения уровень низкого потенциала сигнала полагаем равным нулю, а процесс перехода транзистора из одного состояния в другое — достаточно быстрым.

Логические интегральные микросхемы являются элементами, на основе которых выполняются схемы цифровой техники.

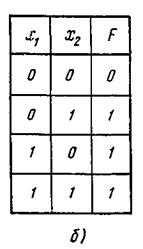
Рис. 3.24, Условное обозначение логического элемента ИЛИ (а), его таблица истинности и временные диаграммы (б, в)

Логический элемент ИЛИ.Логический элемент ИЛИ имеет не­сколько входов и один общий выход. Его условное обозначение пока­зано на рис. 3.24, а.

Логический элемент ИЛИ выполняет операцию логи­ческого сложения (дизъюнкции):

F = x_l + х₂ + х₃ + ... +х_n (3.65)

где F — функция; x₁ х₂, х₃,..., х_п — аргументы (переменные, двоич­ные сигналы на входах).

Здесь функция F = 0, когда все ее аргументы равны нулю, и F = 1 при одном, нескольких или всех аргументах, равных единице.

Работу схемы двухвходового логическо­го элемента ИЛИ иллюстрируют таблица истинности и временные диаграммы, при­веденные на рис. 3.24, б, в. Моделью двух­входового элемента ИЛИ может служить схема с двумя параллельно включенными ключами (см. рис. 3.19, а — г). Если оба ключа выключены (аргументы равны ну­лю), то напряжение на выход равно нулю и F = 0. При одном или двух включенных ключах напряжение на выходе равно Е и F = 1.

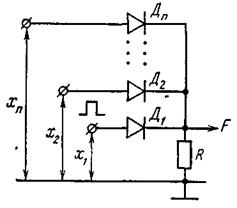
Наиболее просто элемент ИЛИ реали­зуется на диодах (рис. 3.25). Значение F = 1 на выходе создается передачей входного сигнала вследствие отпирания

соответствующего диода. К диодам, для которых входной сигнал равен нулю, прикладывается обратное напряжение, и они находятся в закрытом состоянии.

На практике возможны случаи, когда число входов используемого логического элемента ИЛИ превышает количество входных сигналов. Неиспользуемые входы заземляют. Тем самым исключается возмож­ность прохождения помех через элемент ИЛИ от наводок по неисполь­зованным входам.

Логический элемент И. Логический элемент И также имеет не­сколько входов и один выход. Его условное обозначение показано на рис. 3.26, а.

Логический элемент И выполняет операцию логиче­ского умножения (конъюнкции):

F = x₁ • х₂ • x₃ ...х_п . (3.66)

Здесь функция F = 0, когда хотя бы один из ее аргументов равен нулю, и F = 1 при всех аргументах, равных единице.

Работу схемы двухвходового логического элемента И иллюстри­руют таблица истинности и временные диаграммы, приведенные на рис. 3.26, б, в. Элемент И является схемой совпадения: сигнал «1» на выходе появляется при совпадении сигналов «1» на всех входах. Моделью двухвходового элемента И может служить схема с двумя по

следовательно включенными ключами и источником питания (см. рис. 3.19,д — з).

Простейшая схема элемента И на диодах приведена на рис. 3.27. Отличие от схемы элемента ИЛИ (см. рис. 3.25) заключается в изме­нении полярности включения диодов и наличии резистора R₁, подключенного к шине «+» источника питания.

Схема работает следующим образом. При всех входных сигналах, равных единице, на катодах диодов имеется положительный потен-

циал относительно общей точки и все диоды закрыты. На выходе схе­мы создается напряжение ER₂/(R₁+ R₂), определяющее F =1. При нулевом значении сигнала хотя бы на одном из входов соответ­ствующий диод будет проводить ток и шунтировать резистор R₂ вы­полняющий, как и резистор R в схеме рис. 3.25, роль нагрузки. На­пряжение на выходе при этом определяется падением напряжения на открытом диоде и близко к нулю (F = 0). На рис. 3.27 показан ва­риант, когда x₁=0 и проводит ток диод Д1 Увеличение числа входов с нулевым значением сигнала приво­дит только к увеличению числа прово­дящих диодов, а функция F остается равной нулю. В случае применения логического элемента И, имеющего число входов, большее количества входных сигналов, неиспользуемые входы элемента соединя­ют с шиной «+» источника питания (по­дают сигнал логической «1»). Диоды не­используемых входов будут находиться в закрытом состоянии. Это уменьшает вероятность прохождения помех на вы­ход элемента И от наводок по неисполь-

зованным входам. Поведение логического элемента будет зависеть от комбинации входных сигналов.

Логический элемент НЕ. Логический элемент НЕимеет один вход и один выход. Его условное обозначение показано на рис. 3.28, а. Элемент НЕ выполняет операцию инверсии (о т р и-

ц а н и я), в связи с чем его часто называют логическим и н в е р т о р о м.

Им реализуется функция

F =`х. (3.67)

Сигналу х= 0 на входе соответствует F = 1 и, наоборот, при x= = 1 F = 0.

Работу схемы логического элемента НЕ иллюстрируют таблица истинности и временные диаграммы, приведенные на рис. 3.28, б, в.

Логический элемент НЕ представляет собой ключевую схему на транзисторе (рис. 3.29), анализ которой был дан в § 3.2. При х = 0 (U_вх =0) транзистор закрыт, напряжение U_кэ»E_к, т. е. F = 1. При x= 1 (U_вх = U_вхотп) транзистор открыт, напряжение U_кэ = DU_кэоткр» 0, т. е. F = 0. Открытое состояние транзистора обес­печивается заданием тока базы, вводящего транзистор в режим насы­щения.

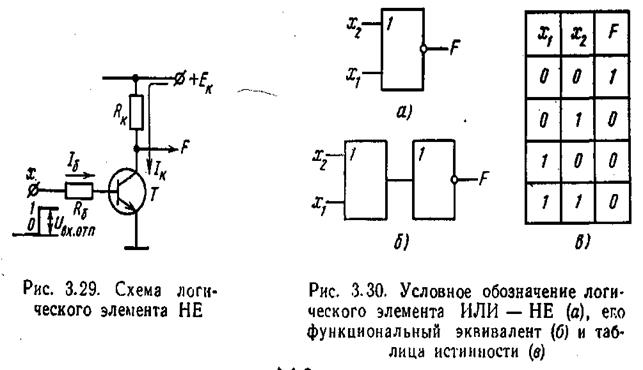
Логический элемент ИЛИ — НЕ. Условное обозначение логичес­кого элемента ИЛИ — НЕ показано, на рис. 3.30, а. Он объединяет элементы ИЛИ и НЕ с очередностью проведения операций, показан­ной на рис. 3.30, б. В связи с этим входным сигналам, равным едини­це, соответствует логический «0» на выходе, а при нулевых сигналах на всех входах F = 1. Для двухвходового элемента ИЛИ — НЕ ука­занное иллюстрирует таблица истинности, приведенная на рис. 3.30, в. Функциональная операция, выполняемая элементом ИЛИ — НЕ при п входах, определяется выражением

F =x₁+ х₂ + х₃ + ∙∙∙ + х_п (3.68)

На рис. 3.31, а приведена схема логического элемента ИЛИ — НЕ, представляющая собой последовательное соединение элемента ИЛИ на диодах и элемента НЕ. Логические схемы подобного сочетания опре­деляют, в частности, класс элементов так называемой д и о д н о транзисторной логики (ДТЛ). Принцип действия эле­мента ясен из диаграмм рис. 3.31, б, где показаны сигналы х₁ и х₂. на входах, сигнал у на выходе элемента ИЛИ и выходная функция F.

Логический элемент И — НЕ. Условное обозначение логического элемента И — НЕ показано на рис. 3.32, а. Ему эквивалентна струк турная схема, показанная на рис. 3.32, б. Логической «1» на всех информационных входах соответствует логический «0» на вы­ходе элемента. При логическом «0» на од­ном из входов создается логическая «1» на выходе. Для двухвходового элемента И — НЕ сказанное отражено в таблице истин­ности на рис. 3.32, в. Логическая функция элемента И — НЕ при п входах отвечает выражению

_________________

F =x_1∙• х_2∙• х₃ ... х_п (3.69)

На рис. 3.33, а приведена схема логи­ческого элемента И — НЕ ДТЛ. Принцип

действия элемента иллюстрируют временные диаграммы рис. 8.33,б. При логических «1» на обоих входах диоды Д₁, Д₂ закрыты. В схе­ме образуется цепь +E_к — R_б — Д' — Д'', которая обеспечивает протекание тока базы /_б » E_к/R_б транзистора. Транзистор открыт и насыщен, F = 0.

При логическом «0» на одном из входов (например, х₁) открыва­ется диод этого входа (Д ₁). Образуется цепь, в которой ток резистора

R_б (рис. 3.33, а) протекает через открытый диод (Д₁) и источник сиг­нала логического «0» (x_t). При этом цепь Д' — Д'' — эмиттерный переход транзистора — оказывается шунтированной цепью с про­водящим диодом. Ток базы транзистора равен нулю, транзистор за­крыт, F = 1.

Поскольку напряжение на открытом диоде входной цепи, а также напряжение входа логического «0» реально больше нуля, точка у на рис. 3.33, а имеет некоторый положительный потенциал относитель­но эмиттера транзистора. В отсутствие диодов Д', Д'' это могло бы привести к отпиранию транзистора. При их введении напряжение между точкой у и эмиттером транзистора будет приложено к диодам, а напряжение U_бэ транзистора близко к нулю. На рис. 3.34 приведена другая схема элемента И–НЕ, реализован­ная на транзисторах. Схемы такого типа образуют класс элементов так называемой транзисторно-транзисторной логики (ТТЛ).

Основой этого класса элементов является использование многоэмит-терного транзистора Т_м .

Подобная замена технологически выгодна, поскольку изготовление многоэмиттерного транзистора в микросхемах не намно­го сложнее, чем изготовление обычного транзистора, а площадь, занимаемая многоэмиттерным транзистором в кристалле полупровод­ника, меньше диодной части элемента И — НЕ ДТЛ. От обычного транзистора многоэмиттерный транзистор отличается наличием не­скольких (например, трех) эмиттерных областей с общими для всего транзистора базовым и коллекторным слоями, При комбинации входных сигналов, когда на одном из входов (например x₁) действует нулевое напряжение (x₁=0), ток через ре­зистор R замыкается по цепи эмиттера этого входа. В базу транзи­стора t₁ток эмиттера I_э1м не ответвляется, так как для направ­ления тока I_км (указано на рис. 3.34 пунктирной стрелкой) сопротив­ление база — эмиттер транзистора Т₁, довольно велико. Транзистор t₁ закрыт. Сигнал на выходе F = 1. Так будет и при нулевом сигнале на большем числе входов элемента.

При наличии на всех входах логической «1» (напряжений, близ­ких к + E_к) все эмиттерные переходы транзистора Т_м будут находить­ся под обратным напряжением, а коллекторный переход — под пря­мым. Ток I_бм будет обусловливать ток I_км, направление которого показано на рис. 3.34 сплошной стрелкой. Транзистор Т₁будет от­крыт, его сигнал F = 0. Таким образом, схема рис. 3.34 выполняет логическую операцию И — НЕ.

Наличие усилительного элемента — транзистора — в логических микросхемах ИЛИ — НЕ и И — НЕ классов ДТЛ и ТТЛ определяет такое их важное преимущество, как сохранение неизменного уровня напряжения, соответствующего логической «1», в процессе передачи сигнала при их последовательном соединении. В связи а этим указан­ные элементы, а также элемент НЕ являются базовыми в микросхе­мотехнике. В общем корпусе выпускаемых микросхем обычно содер­жится несколько элементов одного типа.

Раздел 3