Идея метода резолюций.

1. Пусть требуется доказать в алгебре высказываний, что формула F — тавтология.

2. Рассмотрим отрицание этой формулы 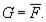Тогда задача переформулируется и станет следующей. Доказать, что формула G — тождественно-ложная.

3. Преобразуем формулу G в конъюнктивную нормальную форму (КНФ)

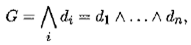
где di— дизъюнкты.

4. Среди дизъюнктов diнайдем резольвентную пару и применим к ней правило резолюции. Полученный новый дизъюнкт, резольвенту, обозначим dn+1и добавим в формулу КНФ для G :

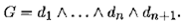
Тем самым получим новую КНФ для G .

5. Если резольвента dn+1= Λ является пустым дизъюнктом, то формула G будет тождественной ложью, задача решена и производим останов. Если нет, то снова найдем, как в п. 4, среди всех дизъюнктов d 1, ..., dn, dn+1резольвентную пару. Применим к ней правило резолюции и добавим полученную резольвенту к имеющимся дизъюнктам. Будем повторять п. 4 и 5, пока не получим пустой дизъюнкт.

Теорема 10.8(о резольвентной паре ). Пусть формула G — тождественно-ложная и представлена в КНФ G = d 1 ∧ ... ∧ dn. Тогда среди дизъюнктов diсуществует резольвентная пара.

Теорема 10.9(о добавлении резольвенты ). Пусть формула G = d 1 ∧ ... ∧ dnпредставлена в КНФ и среди дизъюнктов dj существует резольвентная пара. Тогда добавление в формулу КНФ резольвенты dn+1этой пары является равносильным преобразованием формулы G , т. е.

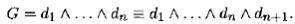
Теорема 10.10(о пустой резольвенте ). Если формула G — тождественно-ложная и представлена в КНФ, то среди всех резольвент исходных дизъюнктов и вновь получаемых дизъюнктов по правилу резолюции существует пустой дизъюнкт.