Правила вывода аксиоматической теории.

1.Правило mp ( modus ponens ):

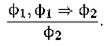
Читается: если имеются две формулы ɸ 1и ɸ 1 ⇒ ɸ 2, то по правилу mp получается формула ɸ 2. При этом формула ɸ 2называется следствием из формул ɸ 1и ɸ 1 ⇒ ɸ 2.

2. Правило связывания квантором общности:

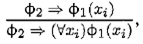
где формула ɸ 2не содержит переменной х i. Чтение правила аналогично предыдущему. Если имеется формула, стоящая над чертой, то получается формула, стоящая под чертой. Вторая формула называется следствием первой по правилу 2.

3. Правило связывания квантором существования:

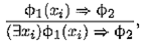
где формула ф2не содержит переменной х i. Чтение правила аналогично предыдущему.

4. Правило переименования связанной переменной: связанную переменную формулы ɸ 1можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в формуле ɸ 1. Чтение этого правила также аналогично предыдущему.

В аксиоматической теории новые формулы получают по правилам вывода из имеющихся формул. Причем если имеющиеся формулы истинны в некоторой интерпретации, то новые формулы будут истинными в той же интерпретации. Что нового появляется в аксиоматической теории по сравнению с логикой предикатов? Синтаксис и семантика, которые имеют место в логике предикатов, полностью переносятся и в аксиоматическую теорию. Но в аксиоматической теории появляется новое семантическое качество — возможность описывать (моделировать) суждения (умозаключения). Этого нет в логике предикатов. В логике предикатов можно в некоторых случаях провести только оценку данной формулы (текста). В аксиоматической теории есть возможность организовать логический процесс: вывод из имеющихся истинных формул (текстов) новых истинных формул с целью получения заданной формулы и одновременно ее оценку. Тем самым логический вывод — оригинальный способ решения задачи оценивания выведенной (заданной) формулы.

Перейдем к строгим определениям главных понятий аксиоматической теории — вывода из гипотез и понятия теоремы.

Определение 10.1.Пусть дано конечное множество формул χ 1, χ 2,… χ m, которые назовем гипотезами. Выводом(доказательством) из этих гипотез назовем последовательность формул

φ 1, φ 2,…,φn, φ ,

где каждая формула последовательности есть или гипотеза, или аксиома, или следствие из формул, стоящих перед данной формулой в последовательности, по одному из правил вывода аксиоматической теории. При этом каждая формула, кроме последней, называется промежуточным результатом, данного вывода. Последняя формула вывода называется окончательным, результатом, вывода. Говорят: формулаɸ выведена из гипотез. Кроме того, получение (появление) каждой формулы вывода называется шагом, вывода.

Кратко вывод (доказательство) из гипотез принято обозначать

χ 1, χ 2,… χ m⊢ φ

Знак ⊢ называется секвенцией .

Если формула φ выводится только из аксиом, не используя никаких гипотез, то она называется теоремой . Говорят: формула φ выведена, или теорема ср доказана в аксиоматической теории. В этом случае пишут: ⊢ φ .

Пример 10.1. Доказать теорему ɸ ⇒ ɸ , т. е. ⊢ ( ɸ ⇒ ɸ ).

На первом шаге вывода рассмотрим первую группу аксиом для случая ɸ 1= ɸ , ɸ 2= ( ɸ ⇒ ɸ ). Будем иметь:

φ 1= (ɸ ⇒ ( ( ɸ ⇒ ɸ ) ⇒ ɸ)).

На втором шаге вывода рассмотрим вторую группу аксиом для случая ɸ 1= ɸ , ɸ 2= ( ɸ ⇒ ɸ ), ɸ 3= ɸ . Будем иметь:

φ 2= (ɸ ⇒ ( ( ɸ ⇒ ɸ ) ⇒ ɸ)) ⇒ ( (ɸ ⇒ (ɸ ⇒ ɸ )) ⇒ ( ɸ ⇒ ɸ )).

На третьем шаге вывода используем первое правило вывода ( mp ) к полученным двум промежуточным результатам вывода. Тогда получим новую формулу:

φ 3= (ɸ ⇒ (ɸ ⇒ ɸ)) ⇒ (ɸ ⇒ ɸ )).

Посмотрев на этот третий результат вывода, видим, что можно снова воспользоваться правилом m р, если предварительно получить соответствующую подформулу, которая стоит в посылке импликации. Поэтому снова рассмотрим первую группу аксиом, но для случая ɸ 1= ɸ , ɸ 2= ɸ Тогда на четвертом шаге доказательства будем иметь:

φ 4= (ɸ ⇒ (ɸ ⇒ ɸ)).

Теперь завершаем доказательство. Применим первое правило вывода к формулам φ 4и φ 3. Получим окончательный результат:

φ 5= ( ɸ ⇒ ɸ ).

Теорема 10.1.Аксиомы аксиоматической теории — общезначимые формулы.

Теорема 10.2.Формула, получающаяся из общезначимых формул по любому из правил вывода, является общезначимой.

Еще важны следующие теоремы, которые также приведем без доказательств.

Теорема 10.3(о дедукции ). Если ɸ 1⊢ ɸ 2, то ⊢ ( ɸ 1⇒ ɸ 2) В общем случае, если справедливо χ 1, χ 2,… χ m⊢ ɸ , имеет место χ 2,… χ m⊢ ( χ 1⇒ ɸ ), т. е. любую гипотезу можно перенести в выводимую формулу в форме посылки соответствующей импликации.

Пример 10.2. Рассмотрим снова задачу: доказать теорему ɸ ⇒ ɸ . Воспользуемся теоремой (метатеоремой) о дедукции. Тогда достаточно доказать, что ɸ ⊢ ɸ , и применить теорему о дедукции. Вывод формулы ɸ из гипотезы ɸ состоит из одного шага ɸ , который является одновременно первым и последним шагом. Тем самым задача решена.

Теорема 10.4.Любая теорема в аксиоматической теории (исчислении предикатов) общезначима.

Теорема 10.5.(о непротиворечивости ). Аксиоматическая теория непротиворечива, т. е. в такой теории нельзя одновременно иметь два доказательства некоторой теоремы и ее отрицания.

Следующая теорема о полноте аксиоматической теории (исчисления предикатов) принадлежит Гёделю.

Теорема 10.6.(теорема Гёделя о полноте ). Всякая общезначимая формула является теоремой в аксиоматической теории.

Вывод . Класс всех теорем аксиоматической теории (исчисления предикатов) совпадает с классом всех общезначимых формул логики предикатов. Но проблема неразрешимости в исчислении предикатов остается в форме отсутствия общего алгоритма поиска вывода (доказательства). Далее рассмотрим современную идею, как можно обойти, в некотором смысле, проблему неразрешимости формальной теории.

Метод резолюций

Подход к определению общезначимости формулы в рамках формальной теории более удобный, чем в рамках логики предикатов. Но в силу неалгоритмичности проблемы разрешимости логики предикатов существуют формулы, для которых неизвестно, как построить их вывод. Во второй половине XX в. американский математик А. Робинсон сформулировал еще один подход к этой алгоритмически неразрешимой задаче. Он предложил перевести проблему в рамки специальной игры с формулами по более простым правилам, чем правила вывода исчисления предикатов. Этот подход был назван методом резолюций. Сначала рассмотрим метод резолюций в применении, к логике высказываний и затем перенесем метод на логику предикатов.

Определение 10.2.Атомарную формулу логики высказываний, или ее отрицание, назовем литерой . Литеры будем обозначать строчными латинскими буквами.

Пример 10.3. Формулы 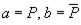являются литерами, а формула Р ⇒ Q не является литерой.

Определение 10.3.Конечная дизъюнкция литер или их отрицаний называется дизъюнктом. Пустой дизъюнкт обозначается Л и означает ложь, или тождественно-равную нулю формулу.

Пример 10.4 . Дизъюнкции:

являются дизъюнктами, а формула — нет.

Определение 10.4.Два дизъюнкта называются резольвентной парой, если существует такая литера, которая участвует в одном дизъюнкте как положительная, а в другом — как отрицательная.

Пример 10.5. Пара дизъюнктов 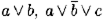— резольвентная, так как литера b участвует в первом дизъюнкте как положительная, а во втором — как отрицательная. Пара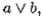 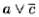не является дизъюнктной парой.

Теорема 10.7.Пусть d 1, d 2— резольвентная пара дизъюнктов вида 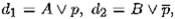где через A , В обозначены члены дизъюнктов с невыделенными литерами. Тогда формула

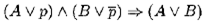
является тавтологией, т. е. тождественно-истинной, или логическим законом.

Доказательство. Если посылка в импликации — ложь, то формула — истина. Если посылка — истина, то каждая скобка — истина. Возможны два случая: р — истина, р — ложь. В первом случае будет: В — истина и, следовательно, заключение импликации ( A ∨ В ) — истина. Во втором случае будет А — истина и, следовательно, снова заключение ( A ∨ В ) — истина. Так как посылка и заключение импликации — истина, то вся формула импликации — истина.

Из этой теоремы следует правило получения из резольвентной пары нового дизъюнкта, который называется резольвентой . Это правило называется правилом резолюции и его записывают в виде

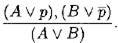
Это правило по виду напоминает правило m р в формальной теории

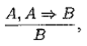
которое, кстати, соответствует следующей тавтологии (логическому закону)

или в виде

Последняя формула соответствует правилу резолюции

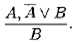
Пример 10.6. Резольвентой для пары 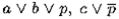будет дизъюнкт a ∨ b ∨ с . Применим правило резолюции к паре 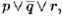получим резольвенту р ∨ r .