ПОСЛЕДОВАТЕЛЬНОСТЬ КОМПЛЕКСНЫХ ЧИСЕЛ. МНОЖЕСТВА

1. Последовательностью комплексных чисел называется неограниченное пронумерованное множество комплексных чисел и обозначается следующим образом: .

Множество точек 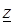комплексной плоскости, удовлетворя­ющее неравенству , называется 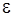-окрестностью точ-
ки .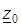

2. Комплексное число 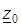называется пределом числовой последовательности , если для любого действительного числа можно указать такой номер 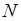, зависящий от 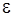, что для всех 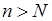будет выполняться неравенство .

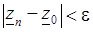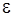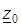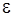Иначе говоря, равенство означает, что как бы мала ни была -окрестность точки , все точки последовательности , начиная с номера , попадут внутрь этой -окрестности.

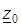Последовательность , имеющая предел , называется сходящейся к числу .

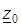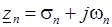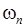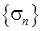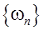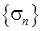Поскольку комплексное число характеризуется парой действительных чисел и , то последовательности комплексных чисел соответствуют две последовательности и действительных чисел. Таким образом, для сходимости последовательности необходимо и достаточно, чтобы сходились последовательности и .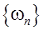

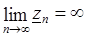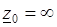3. Если последовательность возрастающая, то удобно считать, что , и говорить, что предел последовательности бесконечен, т.е. последовательность сходится к числу , которое называется бесконечно удаленной точкой. Комплексная плоскость с присоединенной бесконечно удаленной точкой называется расширенной комплексной плоскостью. Для бесконечно удаленной точки понятия действительной и мнимой частей, а также аргумента не определены.

4. Точка 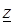называется внутренней точкой множества E точек комплексной плоскости, если существует 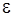-окрестность точки 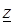, целиком принадлежащая множеству Е.

Множество Е называется областью, если:

а) каждая точка множества Е является внутренней точкой;

б) любые две точки, принадлежащие множеству Е, можно соединить ломаной, состоящей полностью из точек множества Е.

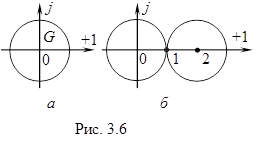
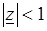Например, множество является областью (рис. 3.6, а), а множество точек не является таковой (рис. 3.6, б), поскольку не удовлетворяет условию б).

Граничной точкой области G называется точка, которая сама не принадлежит области G, но любая 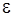-окрестность которой содержит точки G. Например, точка является граничной точкой области 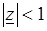(рис. 3.7).

Совокупность граничных точек назовем границей (граничной линией) области и обозначим через .

Область G называется ограниченной, если она лежит внутри некоторого круга конечного радиуса.

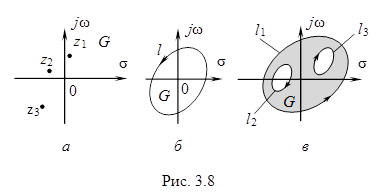
Область может быть определена либо на всей плоскости, либо на всей плоскости за исключением некоторых точек (рис. 3.8, а), либо на части плоскости, ограниченной одной (односвязная область, рис. 3.8, б) или несколькими (многосвязная область, рис. 3.8, в) граничными линиями.

Направление обхода, при котором область G остается слева (рис. 3.8, б и в), называется положительным.