КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
ЭЛЕМЕНТЫ ТЕОРИИ
ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
3.1.1. Определение комплексного числа
Число
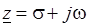
(  и
и 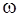 – любые действительные числа, а
– любые действительные числа, а  – мнимая единица
– мнимая единица  ) называется комплексным. Действительные числа
) называется комплексным. Действительные числа  и
и 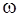 называются действительной и мнимой частями комплексного числа
называются действительной и мнимой частями комплексного числа  и обозначаются как
и обозначаются как
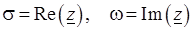 .
.
 Комплексное число
Комплексное число  допускает изображение в виде вектора на комплексной плоскости (рис. 3.1), состоящей из оси действительных чисел (ось
допускает изображение в виде вектора на комплексной плоскости (рис. 3.1), состоящей из оси действительных чисел (ось  ) и перпендикулярной ей оси мнимых чисел (ось
) и перпендикулярной ей оси мнимых чисел (ось 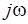 ). Координаты конца вектора равны проекциям вектора на действительную и мнимую оси:
). Координаты конца вектора равны проекциям вектора на действительную и мнимую оси:  и
и 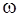 . Иногда удобно комплексное число определять с помощью полярных координат: длины
. Иногда удобно комплексное число определять с помощью полярных координат: длины  и угла
и угла 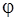 :
:  . Число
. Число  называется модулем комплексного числа
называется модулем комплексного числа  и равно
и равно
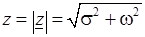 ,
,
а число 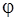 называется аргументом
называется аргументом
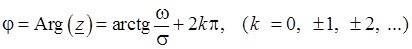 . (3.1)
. (3.1)
Модуль комплексного числа  есть положительное число. Модуль отличен от нуля, если
есть положительное число. Модуль отличен от нуля, если  . Согласно (3.1) аргумент комплексного числа
. Согласно (3.1) аргумент комплексного числа  функция неоднозначная, его главное значение
функция неоднозначная, его главное значение  заключено в пределах
заключено в пределах 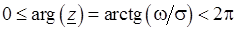 , причем при
, причем при 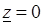 модуль
модуль  , а значение
, а значение  неопределенно.
неопределенно.
Комплексное число можно записать в тригонометрической форме. Поскольку  , то
, то
 .
.
Тот же результат дает преобразование комплекса 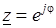 по теореме Эйлера
по теореме Эйлера
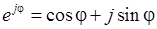 .
.
3.1.2. Свойства комплексных чисел
 1. Равенство. Два комплексных числа
1. Равенство. Два комплексных числа  и
и  равны, если равны порознь их действительные и мнимые части, т.е. равенство
равны, если равны порознь их действительные и мнимые части, т.е. равенство 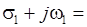
 равносильно равенствам
равносильно равенствам  и
и  .
.
2. Сопряжение. Комплексное число  называется сопряженным к числу
называется сопряженным к числу 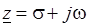 , если
, если  , т.е.
, т.е.  отличается от
отличается от  только знаком мнимой части (знаком аргумента
только знаком мнимой части (знаком аргумента 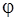 ) (рис. 3.2).
) (рис. 3.2).
 3. Сложение и вычитание. При сложении (вычитании) комплексных чисел
3. Сложение и вычитание. При сложении (вычитании) комплексных чисел  и
и  складываются (вычитаются) отдельно их действительные и мнимые части:
складываются (вычитаются) отдельно их действительные и мнимые части:
 . (3.2)
. (3.2)
Геометрическая интерпретация правила (3.2) приведена на рис. 3.3.
4. Умножение. Оно осуществляется так же, как и умножение многочленов:
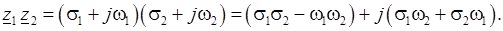
Удобно умножать комплексные числа, заданные в полярных координатах:
 и
и  .
.
В этом случае
 . (3.3)
. (3.3)
Нетрудно видеть, что произведение сопряженных комплексов  и
и  равно квадрату модулей этих чисел:
равно квадрату модулей этих чисел:
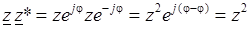 .
.
5. Деление. Оно определяется таким образом:

В полярных координатах это правило записывается проще:
 .
.
6. Возведение в степень и извлечение корня. Из (3.3) следует, что
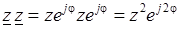 .
.
Аналогично для n умножений
 . (3.4)
. (3.4)
Уравнение (3.4) устанавливает правило возведения комплексного числа в степень 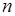 .
.
Рассмотрим операцию извлечения корня из комплексного числа. Пусть 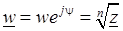 . Применим правило (3.4) к числу
. Применим правило (3.4) к числу  :
:
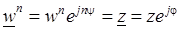 .
.
Два комплексных числа, записанных в полярных координатах, равны друг другу тогда, когда равны их модули
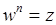 ,
,
а аргументы отличаются на число, кратное  :
:
 .
.
Отсюда следует, что имеется 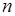 корней с модулем
корней с модулем  и аргументом
и аргументом  , где
, где 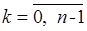 . Тогда
. Тогда
 . (3.5)
. (3.5)
 Дадим геометрическую интерпретацию результата. Как видно из (3.5), все
Дадим геометрическую интерпретацию результата. Как видно из (3.5), все 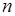 комплексных корней имеют одинаковый модуль, а их аргументы отличаются на
комплексных корней имеют одинаковый модуль, а их аргументы отличаются на 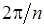 . Следовательно, на комплексной плоскости все они расположены в вершинах правильного п-угольника, вписанного в окружность радиусом
. Следовательно, на комплексной плоскости все они расположены в вершинах правильного п-угольника, вписанного в окружность радиусом  , причем вектор
, причем вектор  расположен под углом
расположен под углом 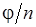 к действительной оси (рис. 3.4).
к действительной оси (рис. 3.4).
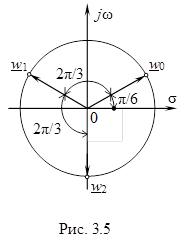 Пример 3.1. Вычислить
Пример 3.1. Вычислить  .
.
Модуль  , a
, a 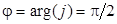 , поэтому
, поэтому
 ,
,  .
.
Или
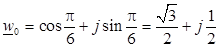 ,
,
 ,
,
 .
.
Расположение корней показано на рис. 3.5.
Дата добавления: 2016-02-14; просмотров: 958;
