ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Говорят, что на множестве Е комплексной плоскости задана функция комплексного переменного (ФКП) 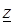 , если задано правило, по которому каждому значению
, если задано правило, по которому каждому значению 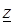 множества Е ставится в соответствие одно или несколько комплексных чисел
множества Е ставится в соответствие одно или несколько комплексных чисел  из множества G значений функции
из множества G значений функции  . Множество G (функция
. Множество G (функция  ) называется многозначным, если каждому значению
) называется многозначным, если каждому значению 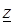 соответствует несколько значений
соответствует несколько значений  .
.
Поскольку комплексное число 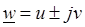 характеризуется парой действительных функций, то задание функции
характеризуется парой действительных функций, то задание функции  комплексного переменного
комплексного переменного 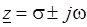 равносильно заданию двух функций
равносильно заданию двух функций 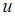 и
и 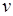 двух действительных переменных
двух действительных переменных  и
и 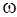 , т. е.
, т. е.
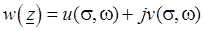 . (3.3)
. (3.3)
Действительные функции 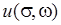 и
и 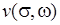 называются действительной и мнимой частями функции
называются действительной и мнимой частями функции 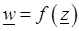 .
.
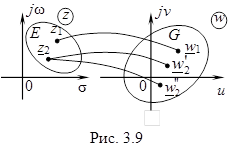 Геометрически задание функции
Геометрически задание функции 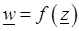 означает, что установлен закон, по которому каждой точке области Е комплексной плоскости
означает, что установлен закон, по которому каждой точке области Е комплексной плоскости 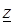 ставится в соответствие одна или несколько точек области
ставится в соответствие одна или несколько точек области 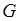 комплексной плоскости
комплексной плоскости  . Таким образом, функция
. Таким образом, функция 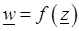 отображает область Е плоскости
отображает область Е плоскости 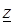 на область G плоскости
на область G плоскости  (рис. 3.9).
(рис. 3.9).
Возможно и обратное отображение: каждой точке 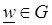 ставится в соответствие одна или несколько точек
ставится в соответствие одна или несколько точек 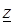 области Е. Это означает, что в области G задана функция комплексного переменного
области Е. Это означает, что в области G задана функция комплексного переменного  :
: 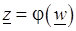 . Она называется обратной по отношению к
. Она называется обратной по отношению к 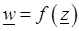 .
.
ПРЕДЕЛ ФКП
Пусть функция  определена и однозначна в некоторой области E плоскости
определена и однозначна в некоторой области E плоскости 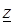 , кроме, быть может, точки
, кроме, быть может, точки 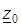 (функция не определена, если содержит выражение вида
(функция не определена, если содержит выражение вида 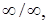
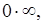
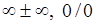 ).
).
Говорят, что функция  имеет предел
имеет предел  при
при 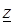 , стремящемся к
, стремящемся к 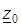 , если для любой сколь угодно малой
, если для любой сколь угодно малой 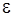 -окрестности точки
-окрестности точки  можно найти
можно найти 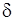 -окрестность точки
-окрестность точки 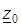 , что для всех точек
, что для всех точек 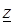 этой
этой 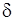 -окрестности (кроме, быть может, самой точки
-окрестности (кроме, быть может, самой точки 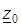 ) соответствующие значения функции
) соответствующие значения функции  будут изображаться точками
будут изображаться точками 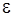 -окрестности точки
-окрестности точки  , т.е.
, т.е. 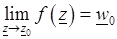 .
.
Согласно (3.6) из существования предела функции  в точке
в точке 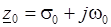 следует существование пределов
следует существование пределов
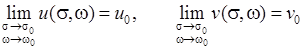 ,
,
причем 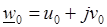 .
.
Дата добавления: 2016-02-14; просмотров: 907;
