КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Если функция дифференцируема не только в данной точке 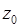, но и в некоторой окрестности этой точки, то она называется аналитической в данной точке.

Функция, аналитическая во всех точках некоторой области, называется аналитической, или голоморфной,в этой области.

Точки плоскости 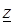, в которых однозначная функция является аналитической, называют правильными, а точки, в которых функция не является аналитической (в частности, точки, в которых не определена) – особыми.

Дадим необходимые и достаточные условия аналитичности функции . Для того чтобы функция 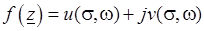, определенная в некоторой окрестности точки 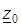, имела производную в этой точке, необходимо и достаточно, чтобы:

1) функци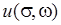и и 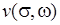были дифференцируемы в точке 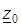по и ;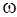

2) в точке 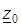выполнялись условия Коши – Римана

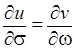и 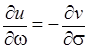. (3.7)

Используя условия Коши – Римана (3.7), можно показать, что

.

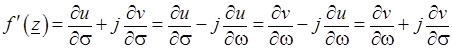Пример 3.2. Определить аналитичность функции

.

Действительная и мнимые части функции

.

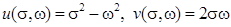Продифференцируем u и v по 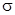и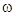

.

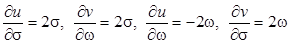Поскольку выполняются условия Коши – Римана для всех точек комплексной плоскости, то функция 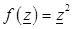аналитична всюду на комплексной плоскости.

Пример 3.3. Определить аналитичность функции .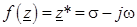

Функция не аналитична, поскольку

,

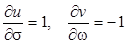и первое из условий (3.7) не выполняется.

ИНТЕГРАЛ ФУНКЦИИ