Пара сил. Момент пары сил

Как известно, сила – основная мера взаимодействия двух тел. Приложим к свободному телу две равные по величине, противоположно направленные силы, которые лежат на параллельных прямых (рис. 3.4). Главный вектор этой системы сил равен нулю, то есть поступательно двигаться это тело не будет. Будет ли оно находиться в равновесии? (Представьте, что вы приложили такую систему сил к водопроводному крану). Какое движение начнется??? Вращательное. То есть надо иметь меру вращательного действия такой системы двух сил:

Система двух равных по величине противоположно направленных сил 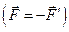, линии действия которых параллельны и не совпадают, называетсяпарой сил (рис. 3.4).

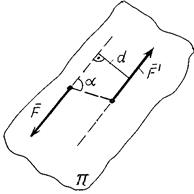Рисунок 3.4

Характеристиками пары сил являются: 1. Плоскость действия пары сил – это плоскость, в которой находятся силы пары. На рис. 3.4 изображена пара сил 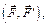где π - это плоскость действия заданной пары сил. Она единственная, поскольку через две параллельных линии можно провести только одну плоскость. 2. Плечо пары сил– это кратчайшее расстояние между линиями действия сил пары. На рис. 3.4 оно обозначено буквой d.

3.Момент пары сил.

Для измерения совместного вращательного действия сил пары 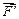и 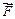относительно произвольной точки О (рис. 3.5) найдем сумму моментов этих сил относительно точки О, вспомнив формулу (3.2):

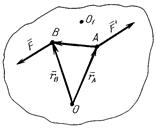Рисунок 3.5

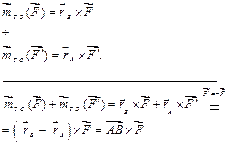
Если поменять точку О на другую точку (напр., О₁), можно убедиться, что результат будет тот же. То есть, вращательное действие пары сил измеряется векторным моментом пары сил, который можно приложить в произвольной точке.

Векторный момент пары сил равен векторному произведению вектора 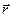, который соединяет точки, в которых приложены силы, на вектор той силы, куда направлен вектор .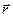

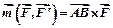, (3.3)

или .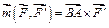

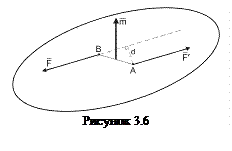
Этот вектор перпендикулярен к плоскости действия пары сил и направлен туда, откуда видно, что вращение тела парой происходит против хода часовой стрелки (рис.3.6).

Величина векторного момента (вектора – момента) пары сил, как модуль векторного произведения, равна 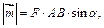где α – угол между векторам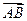и и 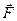(рис. 3.6). Обозначим 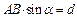, где d – плечо пары.

Тогда 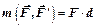. (3.4)

Если пары сил размещены в одной плоскости, то величины их моментов находятся по формуле (3.4), а векторы этих моментов будут коллинеарные. В этом случае целесообразнее пользоваться не векторным понятием момента пары сил, а алгебраическим.

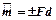. (3.5)

Знак в этой формуле определяется по правилу: если наблюдатель видит попытку пары сил повернуть тело против хода часовой стрелки, берется знак «+», в противном случае знак «–».

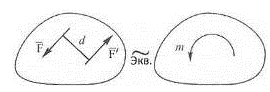Алгебраические моменты пары сил на рисунках показывают дуговыми стрелками (рис 3.7). Отметим также, что единицей измерения момента пары сил, как и момента силы, является .

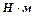Рисунок 3.7.