Две задачи статики для системы пар сил

Сложение пар сил
Пары сил расположены в пространстве
| Геометрический способ | Аналитический способ |
Имеем систему пар сил (рис. 3.11), которые заданы векторными моментами
 Из-за того, что эти свободные вектора действуют в границах одного тела, их можно переносить в одну точку (т. О).
Из-за того, что эти свободные вектора действуют в границах одного тела, их можно переносить в одну точку (т. О).
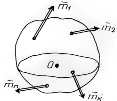 Рисунок 3.11
Складываем векторные моменты по правилу векторного многоугольного (рис. 3.12). Результирующий вектор - замыкающая сторона этого многоугольного (
Рисунок 3.11
Складываем векторные моменты по правилу векторного многоугольного (рис. 3.12). Результирующий вектор - замыкающая сторона этого многоугольного ( 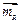 соединяет начало вектора соединяет начало вектора 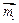 с концом последнего с концом последнего 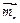 ). ).
 Рисунок 3.12
Рисунок 3.12
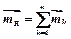 (3.6) (3.6)
| Известно, что вектор в пространстве можно задать его проекциями  .
Спроектировав формулу(3.6) на оси координат, получим проекции момента результирующей пары сил на оси координат .
Спроектировав формулу(3.6) на оси координат, получим проекции момента результирующей пары сил на оси координат
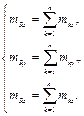 (3.7)
Модуль результирующего вектора равен (3.7)
Модуль результирующего вектора равен
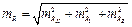 (3.8)
Направление вектора (3.8)
Направление вектора 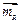 определяют направляющие косинусы определяют направляющие косинусы
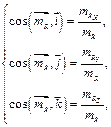 (3.9)
где (3.9)
где 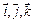 – орты осей Ох, Оу, Оz – орты осей Ох, Оу, Оz
|
Вывод.
| Действие на твердое тело системы пар, произвольно расположенных в пространстве можно заменить действием одной пары, момент которой равен геометрической сумме моментов всех пар системы. |
Дата добавления: 2016-03-15; просмотров: 902;
