Основная теорема статики системы сил произвольно расположенных

в плоскости[1, 2]

Применим основную теорему статики (теорему Пуансо (п. 4.2)) для плоской системы силы. На рисунке 5.1 а показана система трех сил, расположенных в плоскости Оxy. Согласно основной теореме статики, заменим систему сил одной силой – главным вектором 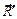и одной парой, момент которой равен главному моменту . Точка О – центр приведения (рис. 5.1 б, в).

а б в

Рисунок 5.1

Известно, что 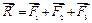. Обозначив проекцию главного вектора на оси координат Оxy, имеем

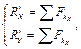
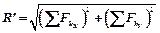. (5.1)

Главный момент в случае плоской системы силы является суммой алгебраических моментов,потому что присоединенные пары сил будут лежать в одной плоскости

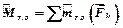. (5.2)

Как будем находить алгебраические моменты? Воспользовавшись формулой (3.1), имеем

.

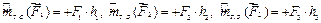Сумма этих моментов будет со знаком «+», поэтому главный момент на рисунке 5.1 в направлен против хода часовой стрелки.

Изложенное выше можно применить не только для трех сил, а для системы «n» сил.

Теорема Пуансо для плоской системы силы.

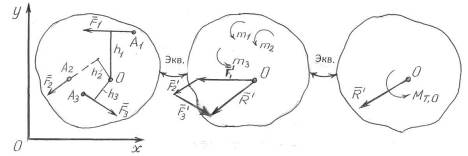
Систему сил, произвольно расположенных в плоскости, можно привести к одной силе 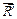, приложенной в центре приведения, и к паре сил, момент которой 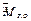алгебраически равен главному моменту системы сил относительно центра приведения.

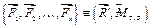. (5.3)