Равновесие составной конструкции

Рассмотрим равновесие системы сил, которые приложены к системе тел, соединенных между собой с помощью шарниров, гибких звеньев (тросов), или таких, которые свободно опираются друг на друга. Силы, действующие на такую систему тел, можно разделить на внешние и внутренние.

Внутренние – силы взаимодействия между телами конструкции.

Внешние – силы, с которыми взаимодействуют тела данной конструкции с другими телами.

Пример. Конструкция состоит из двух твердых тел АС и СДВ, связанных между собой шарниром С (рис. 5.4 а). На конструкцию действует сила 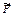, пара сил с моментом М и равномерно распределенная нагрузка интенсивностью q. Для этой конструкции шарнир С – внутренняя связь, а связи, которые присоединяют конструкцию к земле – внешние (шарнир подвижный в точке А и жесткое защемление в точке В).

Определить реакции связей в точках А и В и усилие в шарнире С.

а	б
в	г
Рисунок 5.4

Решение задачи

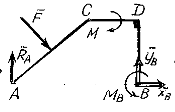
Если объектом изучения взять всю составную конструкцию как абсолютно твердое тело, воспользовавшись аксиомой затвердения (Дополнение А.2) – имеем схему сил, изображенную на рис. 5.4 б. Кроме заданных внешних силовых факторов: силы 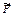, момента М, силы , изображаем реакцию подвижного шарнира А- , направленную вверх (табл. 1.1, п. 4), реакцию жесткого защемления неизвестного направления разложим на две составляющие 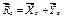и добавим момент пары силы М_В (табл.1.1, п. 5). Таким образом, имеем четыре неизвестных. На конструкцию действует произвольная плоская система сил. На первый взгляд может показаться, что задача статически неопределенная, потому что уравнений равновесия – три; условие (5.10) не выполнено (4>3).

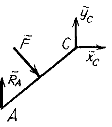
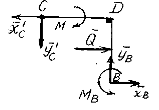
Но из-за того, что конструкция в шарнире С собрана из двух твердых тел АС и СДВ, за объекты изучения можно взять каждую из частей АС и СДВ. Тогда внутреннюю силу реакции шарнира С мы «переведем» в класс внешних сил. При этом воспользуемся аксиомой действия и противодействия (Дополнение А.2) (III-й закон Ньютона). На рисунках 5.4 в и 5.4 г показаны схемы сил, которые действуют на тела АС и СДВ. Это – произвольные плоские системы сил.

Дальше, для схем сил, изображенных на рисунках 5.4 в и 5.4 г, составляем по три уравнения равновесия. Начать лучше из уравнений для схемы 5.4 в, потому что три неизвестные 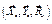легко определить из трех уравнений равновесия (5.5):

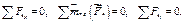
Потом, учитывая, что алгебраические значения 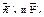равняются алгебраическим значениям 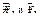, соответственно, составляем уравнения равновесия для схемы сил, которая действует на тело СДВ. Теперь имеем три новых неизвестных 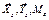. Удачными для их определения будут уравнения равновесия (5.5)

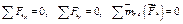
Таким образом, в случае, когда конструкция составлена из нескольких, например n тел, статическую определенность задачи, вместо формулы (5.10) определяем формуле

S ≤ l₁ + l₂ + … + l_n, (5.11)

где S – общее количество неизвестных;

lі – количество уравнений равновесия для і – го тела;

n – количество тел, из которых состоит конструкция.

Вывод: задачи на равновесие системы тел можно решать двумя методами.

Первый метод. Сначала рассматривается равновесие конструкции составленной из системы тел, считая, что внутренние связи затвердели (аксиома затвердения, Дополнение А.2). Позже рассматривается равновесие n –1 тел, из которых составлена конструкция. Составляется необходимое для определения неизвестных сил количество уравнений равновесия, руководствуясь условием статической определенности задачи (формула (5.11)).

Второй метод. Применяя метод разбиения конструкции на части, рассматривается равновесие каждого тела, из которых составлена конструкция. Для каждого тела составляется соответствующее количество уравнений равновесия. Этот метод применен в вышеприведенном примере.

Каким методом пользоваться? Оба методы – равноправные. Можно порекомендовать пользоваться вторым методом, если нужно определить усилия в соединительных элементах. Если спрашивают реакции только внешних связей – пользуются первым методом.

План решения задач вторым методом.

1. На рисунке изображают все заданные силы, которые действует на составную конструкцию. Согласно аксиоме связей (п. 1.4), «отбрасывают» внешние связи, заменяя их соответствующими реакциями связей (табл. 1.1).

2. Выяснив, что количество неизвестных больше количества уравнений равновесия, (которые можно составить для изображенной на рисунке системы сил) конструкцию разбивают на части, из которых она составлена. На следующих рисунках изображают схемы сил, действующие на отдельные свободные тела, заменяя внутренние и внешние связи соответствующими реакциями (табл. 1.1).

3. Проверяем, удовлетворяет ли общее количество неизвестных S и количество уравнений равновесия l₁ + l₂ + … + l_n условию, которое отображает формула (5.11). Если да – задача статически определенная. Приступаем к её решению.

4. Составляем уравнения равновесия для каждого тела, начиная (если это возможно) с тела, для которого количество неизвестных не превышает количества уравнений равновесия.

5. Проверку рационально сделать для всей составной конструкции, считая, что гибкие связи и шарниры затвердели, то есть воспользоваться схемой сил, которую изобразили в первом пункте Плана.