Базовые алгоритмические конструкции
Для выполнения типичных последовательностей действий в алгоритме разработаны базовые алгоритмические конструкции в виде определенного набора блоков и стандартных средств их соединения. К базовым алгоритмическим конструкциям относятся линейные, разветвляющиеся и циклические.
Линейный алтрящ^^
друг за другом* \-> , V
Пример линейного алгоритма приведен на рис. 14.10.
( Начало )
I Ввод А В
X=A* В
IВывод А, В
( Конец ^ Рис. 14.10. Линейный алгоритм
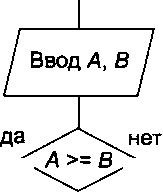
В отличие от линейных алгоритмов, в которых команды выполняются последовательно одна за другой, в разветвляющиеся алгоритмы входит условие, в зависимости от выполнения или невыполнения которого выполняется та или иная последовательность команд (действий). Пример разветвляющегося алгоритма приведен на рис. 14.11.

|
Разввтти>щийш&г0т*ш~~ жцтгърмт,,в котором действия выполняются по сщйойШ| возможных ветвей рёшениязадачй g швадоимосги от выполнения условий. /Vff
В качестве условия в разветвляющемся алгоритме может быть использовано любое понятное исполнителю утверждение, которое может соблюдаться (быть истинным) или не соблюдаться (быть ложным). Такое утверждение может быть выражено как словами, так и формулой. Таким образом, алгоритм ветвления состоит из условия и двух последовательностей команд.
| ( Начало ) |
| X = > | 4 * В |
| X = A +В |
j Вывод А, В j
( Конец ) Рис. 14.11. Разветвляющийся алгоритм
ГТг \ Вычисление
С Начало > —- /71 = 1-2-... /1
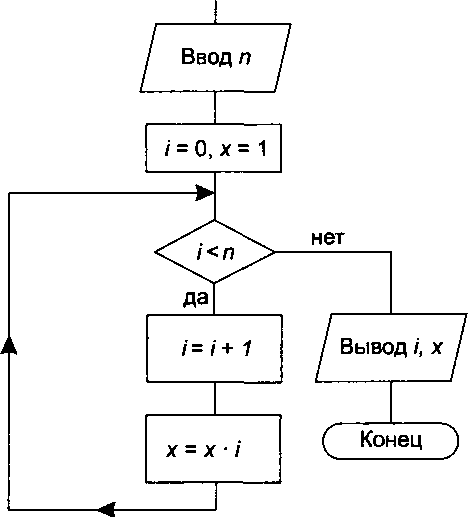 Рис. 14.12. Алгоритм с циклическим элементом
Рис. 14.12. Алгоритм с циклическим элементом
|
Многократные повторения одних и тех же действий обеспечиваются при помощи циклических алгоритмов (рис. 14.12). В цикл входят в качестве составляющих элементов блок проверки условия и блок, называемый телом цикла. Перед началом цикла осуществляются операции присваивания начальных значений тем объектам, которые используются в теле цикла.

|
Слово «многократно» в определении циклического алгоритма не значит «до бесконечности». Организация циклов, не приводящих к остановке в выполнении алгоритма, является нарушением требования его результативности — получения результата за конечное число шагов.
Если тело цикла расположено после проверки условий (цикл с предусловием), то при определенных условиях тело цикла не выполнится ни разу. Такой вариант организации цикла, управляемый предусловием, называется циклом с предусловием (рис. 14.13).
а) Общее обозначение б) Реализация
по ГОСТ 19.701-90
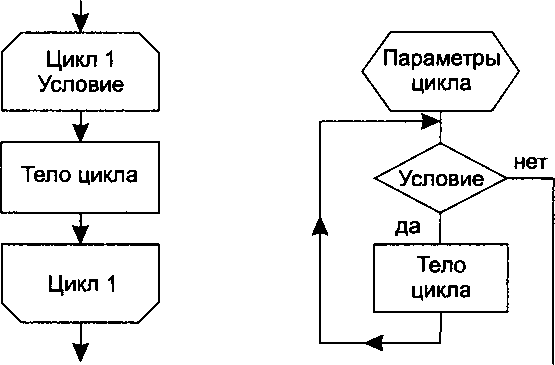 Рис. 14.13. Цикл с предусловием
Рис. 14.13. Цикл с предусловием
|
Другой вариант построения цикла состоит в том, что тело цикла выполняется по крайней мере один раз, и будет повторяться до тех пор, пока условие не станет истинным. Такая организация цикла, когда его тело расположено перед проверкой условия, носит название цикла с постусловием (рис. 14.14). Истинность условия в этом случае является условием выхода из цикла.
а) Общее обозначение б) Реализация
по ГОСТ 19.701-90
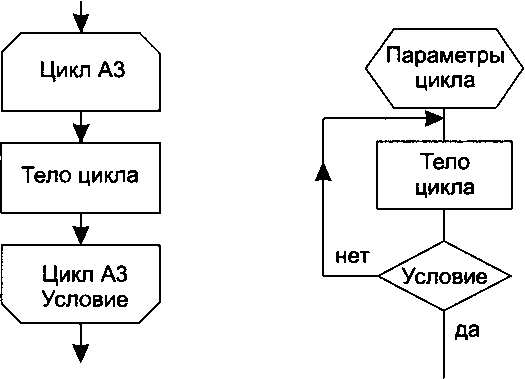 Рис. 14.14. Цикл с постусловием
Рис. 14.14. Цикл с постусловием
|
Таким образом, цикл с предусловием завершается, когда условие ложно, а цикл с постусловием — когда условие становится истинным.
Третий тип циклов, в которых тело цикла выполняется заданное число раз (то есть еще до начала выполнения цикла точно известно, сколько раз он будет выполнен), реализуется с помощью счетчика. В цикле со счетчиком значения счетчика в теле цикла итеративно увеличиваются.
Процесс решения сложной задачи довольно часто сводится к решению нескольких более простых задач методом последовательной детализации. Соответственно, процесс разработки сложного алгоритма может разбиваться на этапы составления отдельных алгоритмов, которые называются вспомогательными. Каждый такой вспомогательный алгоритм описывает решение какой-либо подзадачи.
Процесс построения алгоритма методом последовательной детализации состоит в следующем. Сначала алгоритм формулируется в «обобщающих» блоках, которые могут быть непонятны исполнителю и записываются, как вызовы вспомогательных алгоритмов. Затем происходит детализация, и все вспомогательные алгоритмы детализируются до уровня команд, понятных исполнителю.
Дата добавления: 2016-04-14; просмотров: 1804;
