Представление об алгоритмах
14.1.1. Понятие алгоритма
Во всех сферах своей деятельности, в частности в сфере обработки информации, человек сталкивается с различными способами или методиками решения разнообразных задач. Они определяют порядок выполнения действий для получения желаемого результата — мы можем трактовать это как первоначальное или интуитивное определение алгоритма.
Термин алгоритм происходит от имени средневекового узбекского математика Аль-Хорезми, который еще в 825 году описал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс их выполнения и был назван алгоризмом.
Впоследствии вместо слова алгоризм стали употреблять латинизированное слово алгорисмусу смысл которого состоял в комбинировании четырех операций арифметического исчисления: сложения, вычитания, умножения и деления. Затем алгоритмус преобразовался в алгорифм. Смысл этого понятия чаще всего связывался с алгорифмами Евклида — описаниями процессов нахождения наибольшего общего делителя двух натуральных числе, наибольшей общей меры двух отрезков и т. п.
Под алгоритмом же понимали конечную последовательность точно сформулированных правил, которые позволяют решать различные классы задач. Такое определение алгоритма не является строго математическим, так как в нем не содержится точной характеристики того, что следует понимать под классами задач и под правилами их решения. Таким образом, можно нестрого определить алгоритм как однозначно трактуемую процедуру решения задачи.

^jbmpщфк^ щьштшкомнётшчыт и^отрук^й ^ук&аний)^ ктарт трвтмцвхп^Ш^щ!
Дополнительные требования о выполнении алгоритма за конечное время для любых входных данных приводят к еще одному неформальному определению алгоритма.
Ц^щтт -т это/задаиное на некотором шыке койёцное
Пусть DZ — область (множество) исходных данных задачи Z, a R — множество возможных результатов, тогда мы можем говорить, что алгоритм осуществляет отображение DZ -> R.
Поскольку такое отображение может быть не полным, в теории алгоритмов вводятся понятия частичного и полного алгоритма. Алгоритм называется частичным, если мы получаем результат только для некоторых значений d, принадлежащих DZy и полным, если алгоритм получает правильный результат для всех значений d, принадлежащих DZ.
Сегодня отсутствует одно исчерпывающе строгое определение понятия «алгоритм». Из разнообразных вариантов словесного определения наиболее удачные, видимо, принадлежат российским ученым А. Н. Колмогорову и А. А. Маркову.

|
Алгоритмы можно подразделить на два класса: численные и логические. Численные алгоритмы — это алгоритмы, в соответствии с которыми решение задач сводится к арифметическим действиям.
Логические алгоритмы — это алгоритмы, в соответствии с которыми решение задач сводится к логическим действиям.
Несмотря на различие в определениях, к алгоритмам предъявляется ряд общих требований. Итак, алгоритм должен:
□ содержать конечное количество элементарно выполнимых предписаний, то есть удовлетворять требованию конечности записи;
□ выполнять конечное количество шагов при решении задачи, то есть удовлетворять требованию конечности действий;
□ быть единым для всех допустимых исходных данных, то есть удовлетворять требованию универсальности;
□ приводить к правильному по отношению к поставленной задаче решению, то есть удовлетворять требованию правильности.
Формально строгие определения понятия алгоритма связаны с введением специальных математических конструкций — формальных алгоритмических систем или моделей вычислений, каковыми являются рассматриваемые далее машины Поста и Тьюринга.
14.1.2. Формализация понятия алгоритма посредством машины Поста
Пост рассматривает общую проблему, состоящую из множества конкретных проблем, при этом решением общей проблемы является такое решение, которое определяет ответ для конкретной проблемы.
Например, нахождение решения уравнения Зхх + 9 = 0 — это конкретная проблема, так как в уравнении используются константы, а нахождение решения уравнения а*х + b = 0 — это общая проблема, так как коэффициенты уравнения ^ являются переменными величинами. Алгоритм должен быть универсальным, то есть должен находить решения поставленной задачи в общем виде. Отметим, что сам термин «алгоритм» не используется Э. Постом, его заменяет понятие набора инструкций.
Машина Поста представляет собой абстрактный механизм для выполнения алгоритмов. Этот механизм состоит из двух узлов (рис. 14.1):
□ бесконечной ленты, разделенной на ячейки, каждая из которых может быть помечена или не помечена меткой V;
□ механизма чтения-записи (в дальнейшем — каретка), который может перемещаться вдоль ленты вправо и влево, записывать метку в пустую ячейку, стирать метку в помеченной ячейке и проверять наличие метки в ячейке.
Механизм чтения-записи
V VV V
Лента
Рис. 14.1. Машина Поста
Конкретная проблема задается «внешней силой» (термин Поста) пометкой конечного количества ячеек, при этом очевидно, что любая конфигурация начинается^ и заканчивается помеченной ячейкой. После применения к конкретной проблеме некоторого набора инструкций, решение также представляется в виде набора помеченных и непомеченных ячеек, распознаваемого той же внешней силой.
Пост в 1936 г. предложил набор инструкций, или элементарно выполнимых операций, которые выполняет «работник». В терминах современного состояния компьютерной области этот набор инструкций можно трактовать как минимальный набор битовых операций элементарного процессора. В табл. 14.1 приведены инструкции машины Поста. Латинскими буквами i JJuj2, и т. д. обозначены номера инструкций; M — пометить ячейку, С — стереть метку.
Таблица 14.1. Инструкции машины Поста
|
Программа представляет собой нумерованную последовательность инструкций, причем в инструкции 5 переходы производятся на указанные в ней номера других инструкций. Программа, или набор инструкций, в терминах Э. Поста, является одной и той же для всех конкретных задач, поэтому соотнесена с общей постановкой задачи. Таким образом, Пост формулирует требование универсальности алгоритма. Далее Э. Пост вводит следующие понятия:
□ набор инструкций применим к общей проблеме, если для каждой конкретной проблемы не возникает коллизий в инструкциях 1 и 2, то есть программа никогда не стирает метку в пустой ячейке и не устанавливает метку в помеченной ячейке;
□ набор инструкций заканчивается, если после конечного количества инструкций выполняется инструкция 6.
Начальное состояние машины Поста полностью определяется двумя факторами: положением каретки (на какой из ячеек она находится) и состоянием ленты (наличием на ленте помеченных ячеек).
В зависимости от начального состояния машины Поста могут быть три варианта выполнения одной и той же программы:
1. В ходе выполнения программы машина доходит до невыполнимой инструкции (печатания метки в непустой ячейке или стирания метки в пустой ячейке). Происходит безрезультатная остановка машины.
2. В ходе выполнения программы машина доходит до инструкции Стоп. Происходит результативная остановка.
3. Работа машины продолжается бесконечно.
Машина Поста оперирует натуральными числами, которые представляются в непозиционной системе счисления (то есть 0 обозначается одной помеченной ячейкой, 1 — двумя идущими подряд помеченными ячейками, и т. д.). В общей форме натуральное число п представляется п + 1 смежными помеченными ячейками.
Пример. Рассмотрим следующую программу для машины Поста: / -> 4
2. СЗ
3. стоп
4. -> 2
Зададим такое начальное состояние машины, которое показано на рис. 14.2.

|
| V |
| Рис. 14.2. Начальное состояние машины Поста |
Поскольку каретка находится на пустой ячейке, первая команда программы вызывает переход на команду с номером 4. При этом каретка не меняет своего положения, и состояние ленты также не меняется (метка не ставится и не стирается).
Команда с номером 4 вызывает перемещение каретки на одну позицию вправо (теперь каретка находится на помеченной ячейке) и передачу управления команде 2.
Команда 2 стирает метку в текущей ячейке и передает управление команде 3.
Команда 3 останавливает работу машины.
14.1.3. Формализация понятия алгоритма посредством машины Тьюринга
Алан Тьюринг в 1936 г. опубликовал в трудах Лондонского математического общества статью «О вычислимых числах в приложении к проблеме разрешения», которая наравне с работами Поста и Черча лежит в основе современной теории алгоритмов. Предыстория появления этой работы связана с формулировкой Давидом Гильбертом на Международном математическом конгрессе в Париже в 1900 г. нерешенных математических проблем. Одной из них была задача доказательства непротиворечивости системы аксиом обычной арифметики, которую Гильберт в дальнейшем уточнил как «проблему разрешимости» — нахождение общего метода для определения выполнимости данного высказывания на языке формальной логики.
Статья Тьюринга как раз и давала ответ на эту задачу, но значение статьи Тьюринга выходило далеко за ее рамки. Вот как охарактеризовал эту работу Джон Хопкрофт (известный американский ученый в области теории вычислительных систем): «Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, то есть процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга».
Машина Тьюринга является расширением модели конечного автомата, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу. То есть «конструктивно» машина Тьюринга, так же как и машина Поста, состоит из двух основных узлов: ленты с ячейками и каретки.
Решаемая проблема задается путем записи на ленту конечного количества символов Sit образующих слово в алфавите St где е — это специальный пустой символ, показывающий отсутствие любого символа алфавита S в ячейке (рис. 14.3).
| е | S1 | S2 | S3 | S4 | Sn | е |
| Рис. 14.3. Машина Тьюринга |
В отличие от машины Поста, в машине Тьюринга каретка неподвижна, а лента проматывается лентопротяжным механизмом на одну ячейку вправо или влево. Состояния машины Тьюринга обозначаются как q{ и принадлежат множеству состояний Q. Управляется машина при помощи функции переходов, которая называется программой машины Тьюринга и может быть задана в виде таблицы или ориентированного графа. При этом при задании функции переходов используются как команды лентопротяжному механизму (смещение ленты на одну ячейку вправо, смещение ленты на одну ячейку влево, перемотка в начало, останов), так и команды каретки (запись нового символа, чтение символа, запись пустого символа). После задания проблемы машина переводится в начальное состояние (обозначаемое как #о), и лента проматывается так, чтобы каретка находилась у самого левого непустого символа, после чего в соответствии с указанной функцией переходов машина начинает заменять обозреваемые символы, передвигать каретку вправо или влево и переходить в другйе состояния (путем стирания текущего символа и замены его новым). Останов машины происходит в том случае, если для пары «состояние машины — символ в текущей ячейке» (qb Sj) функция перехода не определена или получена команда останова.
Тьюринг высказал предположение, что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной в предложенной им модели вычислений. Это предположение известно как тезис Черча—Тьюринга. Каждый компьютер может моделировать машину Тьюринга, для этого достаточно моделировать операции перезаписи ячеек, сравнения и перехода к другой соседней ячейке с учетом изменения состояния машины. Значит, он может моделировать алгоритмы в машине Тьюринга, и из этого тезиса следует, что все компьютеры, независимо от мощности, архитектуры и других особенностей, с точки зрения принципиальной возможности решения алгоритмически разрешимых задач эквивалентны.
14.1.4. Современная теория алгоритмов
Начальной точкой отсчета современной теории алгоритмов можно считать теорему о неполноте символических логик, доказанную немецким математиком Куртом Геделем в 1931 г. В этой работе было показано, что некоторые математические проблемы не могут быть решены алгоритмами определенного класса.
Общность результата Геделя связана с вопросом о том, совпадает ли использованный им класс алгоритмов с классом всех алгоритмов в интуитивном понимании этого термина. Эта работа дала толчок к поиску и анализу различных формализа- ций понятия «алгоритм».
Первые фундаментальные работы по теории алгоритмов были опубликованы в середине 1930-х гг. Аланом Тьюрингом, Алоизом Черчем и Эмилем Постом. Предложенные ими машина Тьюринга, машина Поста и класс рекурсивно-вы- числимых функций Черча были первыми формальными описаниями алгоритма, опирающимися на строго определенные модели вычислений. Сформулированные гипотезы Поста и Черча—Тьюринга постулировали эквивалентность предложенных ими моделей вычислений, как формальных систем, и интуитивного понятия алгоритма. Важным развитием этих работ стала формулировка и доказательство существования алгоритмически неразрешимых проблем.
В 1950-х гг. существенный вклад в развитие теории алгоритмов внесли работы Колмогорова и основанный на теории формальных грамматик алгоритмический формализм Маркова — так называемые нормальные алгоритмы Маркова. Формальные модели алгоритмов Поста, Тьюринга и Черча, равно как и модели Колмогорова и Маркова, оказались эквивалентными в том смысле, что любой класс проблем, разрешимых в одной модели, разрешим и в другой.
Появление доступных ЭВМ и существенное расширение круга решаемых на них задач привели в 1960—1970-х гг. к практически значимым исследованиям алгоритмов и вычислительных задач. На этой основе впоследствии выделилось несколько разделов теории алгоритмов (рис. 14.4).
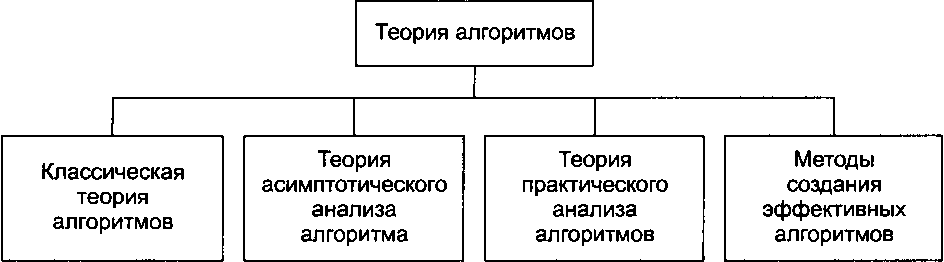 Рис. 14.4. Разделы современной теории алгоритмов
Рис. 14.4. Разделы современной теории алгоритмов
|
Классическая теория алгоритмов: формулировка задач в терминах формальных языков; понятие задачи разрешения; описание сложностных классов задач; формулировка в 1965 г. Эдмондсом проблемы P = NP; открытие класса TVP-полных задач и его исследование; введение новых моделей вычислений — алгебраического дерева вычислений (Бен-Op), машины с произвольным доступом к памяти, схем алгоритмов Янова, стандартных схем программ Котова и др.
Теория асимптотического анализа алгоритмов: понятие сложности и трудоемкости алгоритма; критерии оценки алгоритмов; методы получения асимптотических оценок, в частности, для рекурсивных алгоритмов; асимптотический анализ трудоемкости или времени выполнения; получение теоретических нижних оценок сложности задач. В развитие этой теории внесли существенный вклад Кнут, Ахо, Хопкрофт, Ульман, Карп, Мошков, Кудрявцев и др.
Теория практического анализа вычислительных алгоритмов: получение явных функций трудоемкости; интервальный анализ функций; практически значимые критерии качества алгоритмов; методики выбора рациональных алгоритмов. Основополагающей работой в этом направлении, очевидно, следует считать фундаментальный труд Д. Кнута «Искусство программирования для ЭВМ».
Методы создания эффективных алгоритмов включают в себя множество алгоритмов, среди которых динамическое программирование, метод ветвей и границ, метод декомпозиции, «жадные» алгоритмы, специальные структуры данных и пр.
Обобщая исследования в различных разделах теории алгоритмов, можно выделить следующие основные задачи и направления развития, характерные для современной теории алгоритмов:
□ формализация понятия «алгоритм» и исследование формальных алгоритмических систем (моделей вычислений);
□ доказательство алгоритмической неразрешимости задач;
□ формальное доказательство правильности и эквивалентности алгоритмов;
□ классификации задач, определение и исследование сложностных классов;
□ доказательство теоретических нижних оценок сложности задач;
□ получение методов разработки эффективных алгоритмов;
□ асимптотический анализ сложности итерационных алгоритмов;
□ исследование и анализ рекурсивных алгоритмов;
□ получение явных функций трудоемкости алгоритмов;
□ разработка классификаций алгоритмов;
□ исследование емкостной (по ресурсу памяти) сложности задач и алгоритмов;
□ разработка критериев сравнительной оценки ресурсной эффективности алгоритмов и методов их сравнительного анализа.
Дата добавления: 2016-04-14; просмотров: 2472;
