Представление и обработка данных разного типа
14.4.1. Общее представление о типах данных
Алгоритм, реализующий решение некоторой конкретной задачи, всегда работает с данными.
С точки зрения процесса обработки данные могут быть входными (исходными), выходными {результирующими) и промежуточными.
Данные подразделяют на переменные и константы.

|
Например, для алгоритма вычисления площади круга необходимы две переменные: переменная Ry в которую будет заноситься значение радиуса окружности, и переменная Sy в которую будет помещено значение площади круга, вычисленное по формуле S = TiR2. Число тт — константа.
|
Каждая переменная или константа в алгоритме должна иметь свое уникальное имяу которое задается идентификатором. Идентификатор представляет собой последовательность букв и цифр, начинающуюся с буквы.
С данными тесно связано понятие типа данных. Типы данных вводятся для того, чтобы использовать их в различных алгоритмах обработки. Следовательно, нужно иметь еще и множество операций, которые можно применять к данным того или иного типа.
Тип данных характеризует множество значений, к которым относится константа и которые может принимать переменная или выражение. Например, если переменная i в алгоритме может принимать только значение из множества целых чисел, то эта переменная относится к целому типу данных.

|
Типы данных принято делить на простые (базовые) и структурированные. К структурированным данным относят наборы данных, имеющие разное представление: массивы, символьные цепочки, деревья, графы.
- шш кщститы
Наиболее общий метод получения структурных типов заключается в объединении элементов произвольных типов в одной переменной. Причем сами эти элементы могут быть в свою очередь структурными. Например, это могут быть комплексные числа, состоящие из вещественной и мнимой частей, или параметры точки, определяемые координатами и цветом.
14.4.2. Базовые типы данных
К базовым типам данных относятся следующие типы:
□ целые (INTEGER) — подмножество допустимых значений из множества целых чисел;
□ вещественные (REAL) — подмножество допустимых значений из множества вещественных чисел;
□ логические (BOOLEAN) — множество допустимых значений состоит всего из двух значений, истина и ложь.
□ символьные (CHAR) — буквы, цифры, знаки препинания и т. д.

Тип INTEGER задает подмножество целых чисел, диапазон которого зависит от такой характеристики компьютера, как размер машинного слова. Если для представления в компьютере целых чисел х используется п разрядов (причем один из них отводится под указание знака числа), то допустимые числа должны удовлетворять условию -2"-1 < х < 2"-1 (Приведенный диапазон значений целых чисел в я-разрядном представлении соответствует одной из возможных форм кодирования. Чаще всего на практике используется другая форма кодирования, при которой модуль минимального отрицательного числа на единицу больше модуля
максимального положительного числа, т. е. -(2"-1) < х < (2"_1)-1.) Считается, что все операции над данными этого типа выполняются точно и соответствуют обычным правилам арифметики. Если результат выходит за пределы допустимых значений, то вычисления прерываются. Такое событие называется переполнением.
Для целых чисел без знака может быть определен дополнительный стандартный тип — целое без знака (в некоторых языках программирования, кроме того, можно определить тип «натуральное число»), задающий подмножество целых неотрицательных чисел (соотвественно, подмножество натуральных чисел). Если для представления целых без знака используется п разрядов, то переменным такого типа можно присваивать значения, удовлетворяющие условию 0 < х < 2"-1 (соответственно, 0 < х < 2"-1 или 0 < х < 2", в зависимости от реализации).
Пример. Целые числа обычно применяют в тех случаях, когда необходимо записать некоторое значение, поддающееся подсчету: количество предметов, лет, дней, записей, слов. В алгоритмах тип INTEGER так же используют для подсчета итераций цикла или нумерации элементов массива.
Тип REAL обозначает подмножество вещественных чисел, границы изменения которых также определяются характеристиками конкретного компьютера. И если считается, что арифметика с данными типа INTEGER дает точный результат, то допускается, что аналогичные действия со значениями типа REAL могут быть неточными в пределах ошибок округления, вызванных вычислениями с конечным числом цифр. Это принципиальное различие между типами REAL и INTEGER.
Пример. Тип REAL обычно применяется для представления величин, которые можно измерить прямым измерением (веса, температуры), а также результатов деления, в общем, любых величин, имеющих дробную часть.
Два значения типа BOOLEAN обозначаются идентификаторами со значениями истина (TRUE) и ложь (FALSE). Операции над данными этого типа подчиняются правилам булевой алгебры.
Пример. Тип BOOLEAN играет важную роль при составлении алгоритмов: именно на основе значений, которые принимают переменные или выражения этого типа, осуществляется управление ходом выполнения программы (алгоритма).
В базовый тип CHAR входит множество печатаемых символов и символов- разделителей в соответствии с кодом ASCII.
Пример. Тип CHAR является основой всех простых и сложных типов, содержащих текст (строк, массивов и коллекций строк, записей).
К переменным типа REAL и INTEGER применимы арифметические операции, такие как сложение (+), вычитание (-), умножение (*) и деление (/), к переменным типа BOOLEAN — логические операции, к символьным переменным — операция конка
тенации («склеивания») последовательностей символов. Операции отношения или сравнения применяются к данным любого типа, но правила их применения различны.
14.4.3. Представление и обработка данных в виде структур (массив, запись)
Наиболее известная структура данных — массив. Массив представляет собой упорядоченную структуру однотипных данных, которые называются элементами массива. Массив подходит для решения задач, в которых накапливаются и подлежат обработке данные одного и того же типа.
Доступ к каждому элементу массива осуществляется с помощью индекса. В общем случае индекс — это порядковый номер элемента в массиве.
Массивы могут быть как одномерными (адрес каждого элемента определяется значением одного индекса), так и многомерными (адрес каждого элемента определяется значением нескольких индексов).
Другим известным структурным типом данных является запись. Элементы записи называются полями. Примером данных такого типа может быть запись «Информация о студенте». Для представления такого типа в каждом языке программирования существуют встроенные средства языка, но, кроме того, такой тип (или переменная такого типа) может быть представлен графически (рис. 14.15).
| Иванов | Петр | Николаевич | 2239/22 |
| Рис. 14.15. Графическое изображение записи данных в массиве |
Из записей могут формироваться массивы. Такое сочетание двух этих структурных типов часто встречается при обработке данных, извлеченных из баз данных.
В качестве примера рассмотрим алгоритм обработки двухмерного массива. Аналогом двухмерного массива в математике является матрица. Общий вид матрицы Л размерности M х Доследующий:
ап аУ1 ... аш
| Л = i-1...М, |
а2\ а22 ••• а2 N aM 1 аМ2 ••• aMN
Для матрицы размерностью Nx N (квадратной матрицы) определены понятия главной и побочной диагоналей. Элементы главной диагонали -г- {a^i = 1..JV}, а элементы побочной — {fluN-i+n, i — I...N}.
Пример. Пусть необходимо построить матрицу, элемент которой at> вычисляется как (г + j)2, а элементам главной диагонали присвоить значение 0.
Для решения поставленной задачи воспользуемся двухмерным массивом целых чисел. На первом этапе происходит построение вложенного цикла для расчета элементов и заполнения массива. На втором этапе элементам главной диагонали присваиваются нулевые значения.
Блок-схема такого алгоритма приведена на рис. 14.16 (ЛГ— размерность массива, IwJ — индексы массива).
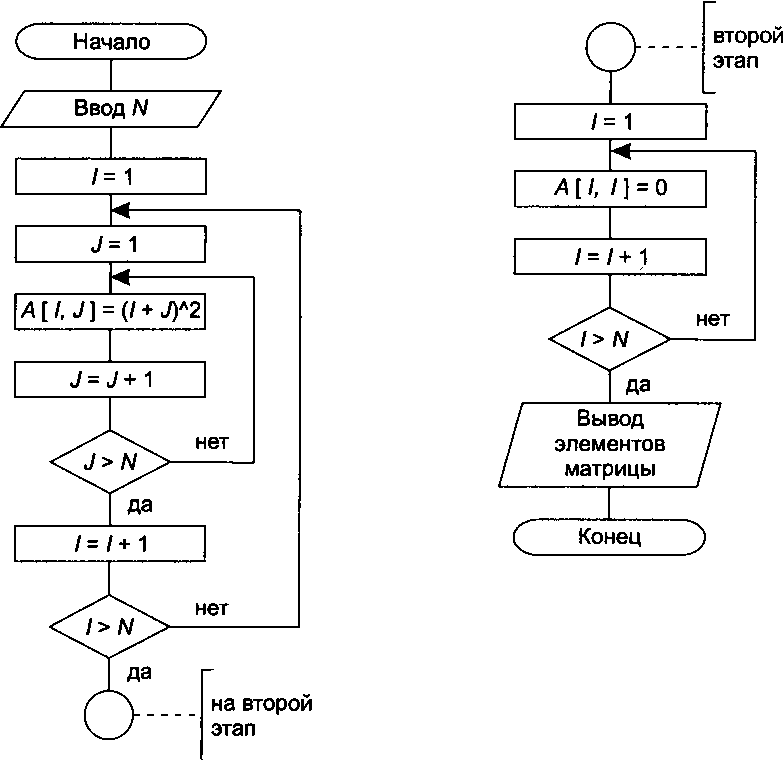 Рис. 14.16. Блок-схема алгоритма обработки двухмерного массива
Рис. 14.16. Блок-схема алгоритма обработки двухмерного массива
|
14.4.4. Представление и обработка данных в виде символьных цепочек
Символьные цепочки с точки зрения физической организации представляют собой обыкновенные массивы типа CHAR. Особенность этого типа данных состоит в том, что символьный массив в подавляющем большинстве случаев является осмысленным текстом, а значит, имеет логическую структуру: разделен на слова, предложения, строки и абзацы. Поэтому алгоритмы обработки символьных цепочек почти всегда включают в себя поиск специальных символов-разделителей, разделение текста на логические единицы (слова, предложения, строки) и выполнение операций (подсчет, сортировка, поиск и замена) над этими единицами.
В качестве примера рассмотрим задание на определение количества слов в последовательности символов. Определим слово как часть последовательности (ненулевой длины), ограниченную с двух сторон (либо только справа или слева) символом пробела.
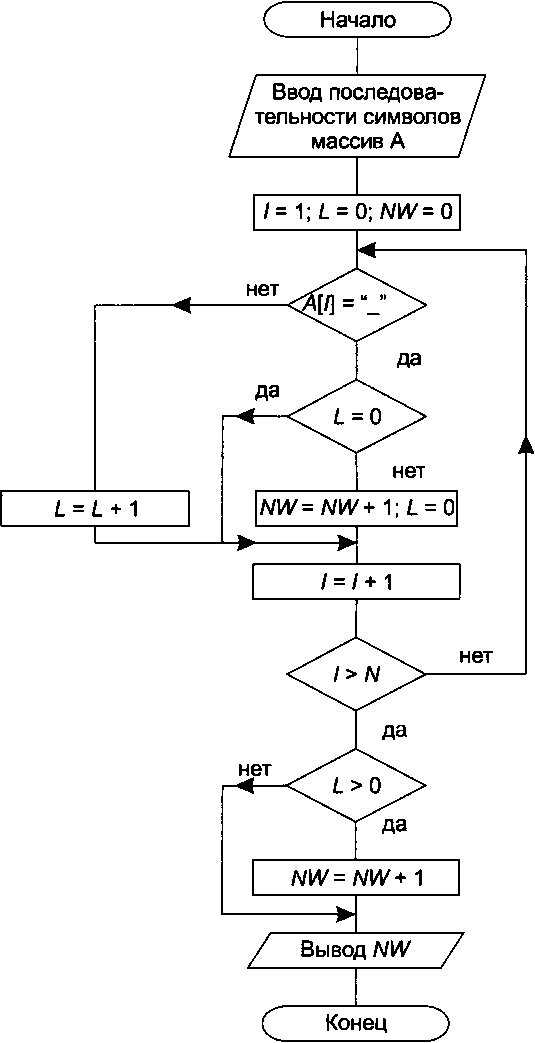 Рис. 14.17. Блок-схема алгоритма определения количества слов в последовательности символов
Рис. 14.17. Блок-схема алгоритма определения количества слов в последовательности символов
|
Для решения задачи разместим обрабатываемую последовательность в массиве размерностью N (где N- длина последовательности). При построении алгоритма необходимо учесть, что последовательность может начинаться или заканчиваться пробелами, причем в потоке символов может встретиться несколько смежных пробелов.
Блок-схема алгоритма приведена на рис. 14.17. Здесь L — длина очередного слова, NW- количество слов в последовательности, знак пробела обозначен символом подчеркивания (_).
14.4.5. Представление и обработка данных в виде одно- и двусвязных списков
Структура данных, в которой объекты расположены в линейном порядке, называется связным списком. Однако в отличие от массива, в котором этот порядок определяется индексами, порядок в связном списке определяется указателями на объекты.
Элемент (узел) связного списка, помимо полей с данными, имеет поле next, в котором содержится указатель на следующий элемент списка. Если это последний элемент списка, поле next принимает нулевое значение. Помимо своих элементов, каждый список содержит указатель head на первый элемент списка. Если этот указатель равен 0, значит, список пуст. Поскольку этот указатель относится к списку в целом и не содержит в себе данных, на рис. 14.18, на котором схематически показан односвязный список, указатель не заключен в прямоугольник.
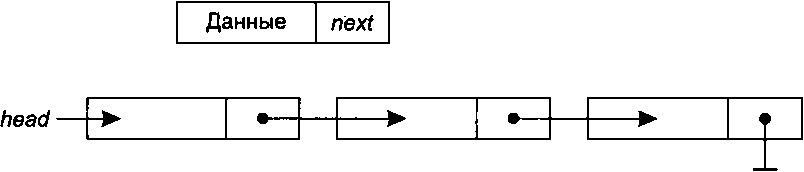 Рис. 14.18. Односвязный список
Рис. 14.18. Односвязный список
|
Односвязный список отличается тем, что пройти по нему можно только в одном направлении — от начала в конец списка. Это оказывается достаточно неудобно, поэтому гораздо большее распространение получили двусвязные списки (рис. 14.19), отличающиеся тем, что их узлы содержат по два указателя — на следующий (next) и на предыдущий (prev) элементы списка. Помимо указателя head на первый элемент списка, может существовать также указатель tail на последний элемент списка.
 Рис. 14.19. Двусвязный список
Рис. 14.19. Двусвязный список
|
, Частный случай двусвязного списка — замкнутый (кольцевой) список, указатель next последнего элемента которого указывает на первый элемент, а указатель prev первого элемента — на последний элемент списка.
Главная особенность списка — быстрое выполнение операций вставки и удаления в произвольном месте списка. Эти операции требуют модификации указателей максимум у трех узлов: узла, над которым выполняется операция, и двух окружающих узлов. Схематично эти операции и изменения значений указателей показаны на рис. 14.20.

|
 Удаление
Рис. 14.20. Вставка и удаление в двусвязных списках
Удаление
Рис. 14.20. Вставка и удаление в двусвязных списках
|
Алгоритм этих операций, приведенный на рис. 14.21 и 14.22, показывает, насколько простыми являются алгоритмические операции со списками.
( Начало"^)
Ввод L1 х
x.next = L.head---
false
|
| x.prev = 0 |
Вывод L
Входные данные: L — список
х — вставляемый элемент (узел)
Поле next элемента х теперь указывает на первый элемент списка, поскольку мы присвоили ему значение указателя head
Список не пустой, и указатель head указывает на следующий узел?
Указатель prev бывшего первого элемента списка теперь указывает на вставляемый элемент х
Указатель head списка теперь указывает на вставленный элемент х
Поскольку х в списке первый, его указатель prev не указывает ни на какой элемент
Выходные данные: L — список со вставленным элементом х
Q Конец )
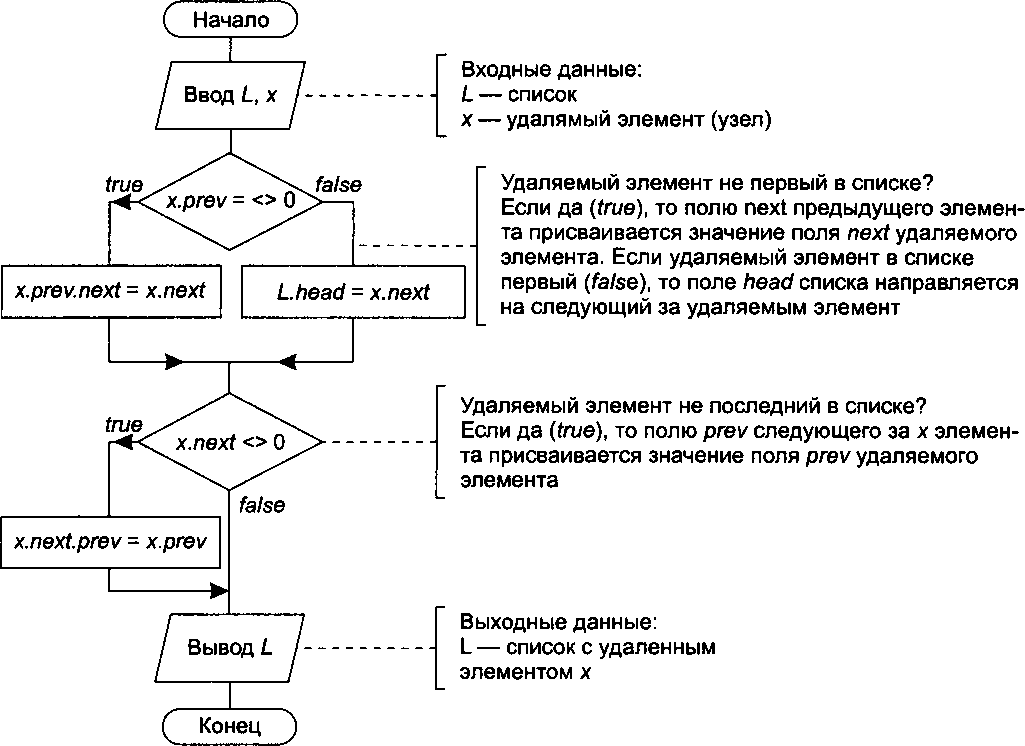 Рис. 14.22. Удаление элемента списка
Рис. 14.22. Удаление элемента списка
|
14.4.6. Представление и обработка данных в виде деревьев
Элементы данных могут образовывать и более сложные структуры, чем линейный список. Часто данные, подлежащие обработке, образуют иерархическую структуру, которую необходимо отобразить в памяти компьютера и, соответственно, описать в структурах данных. Такая структура получила название дерева. Каждый элемент такой структуры, называемый узлом, может содержать ссылки на элементы более низкого уровня иерархии, а может быть, и на объект, находящийся на более высоком уровне иерархии. Узел, находящийся на самом верхнем уроне иерархии, называется корневым.
|
Корень дерева — это единственный узел, не имеющий непосредственного предка.
Имеется множество типов деревьев. Важнейшим с точки зрения информатики подмножеством структуры типа дерева является подмножество бинарных деревьев поиска. У бинарного дерева каждый узел имеет не более двух дочерних узлов, причем левый и правый узлы различаются. Каждый узел содержит несколько полей: поля значения, хранящегося в узле, и полей, указывающих на левый и правый потомки данного узла, а также на родительский узел. Бинарным деревом поиска его делает следующее свойство: значения в узлах дерева располагаются таким образом, что в любой момент для любого узла х значения всех узлов в его левом поддереве не превышают значения узлах, а значения всех узлов в его правом поддереве не меньше значения узла х. На рис. 14.23 показано несколько деревьев. Числа в кружках отражают значения данных, хранящихся в узлах дерева. Дерево на рис. 14.23, а не является бинарным, так как у узла 5 есть три дочерних узла. Дерево на рис. 14.23, б является бинарным, но не является деревом поиска, так как узел 2 является правым дочерним узлом по отношению к узлу 3, нарушая свойство дерева поиска. Дерево
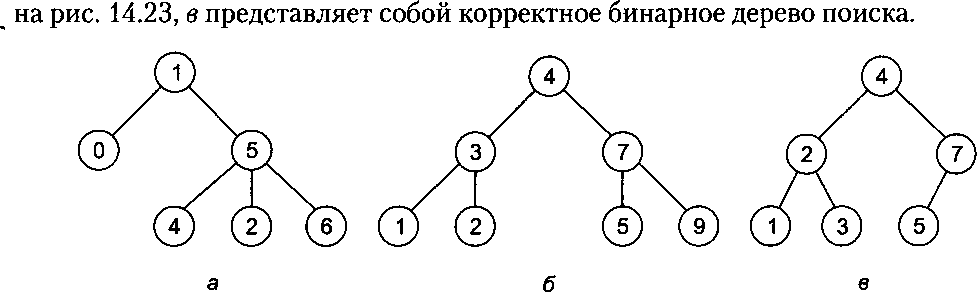 Рис. 14.23. Виды деревьев
Рис. 14.23. Виды деревьев
|
На рис. 14.24 изображено возможное представление бинарного дерева поиска с использованием полей указателей. На этом рисунке, как и на предыдущем, цифры представляют собой значения, хранящиеся в каждом из элементов дерева, а стрелки показывают, как при помощи указателей каждый узел дерева связан со своими правым и левым поддеревьями, а также с родительским узлом. Так, для узла со значением 2 буквой а помечен указатель, связывающий его с родительским узлом, а буквами Ьис — указатели, связывающие этот узел, соответственно, с его левым и правым поддеревьями.
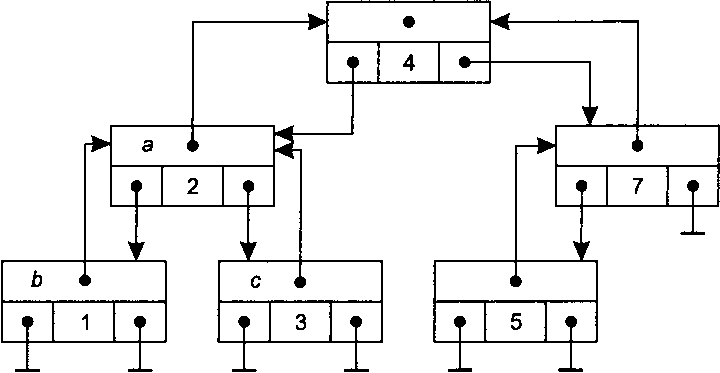 Рис. 14.24. Бинарное дерево поиска
Рис. 14.24. Бинарное дерево поиска
|
Посетить все узлы дерева очень легко с помощью рекурсивной процедуры обхода. Основной вариант обхода бинарного дерева — симметричный обход дерева, когда для каждого узла сначала рекурсивно выполняется посещение его левого поддерева, затем — самого узла, а после этого — узлов его правого поддерева. Для дерева на рис. 14.24 симметричный обход дает следующую последовательность узлов: 1,2, 3,4,5,7. Как видите, таким образом можно получить отсортированную последовательность значений узлов.
Два других распространенных метода обхода дерева — обход в прямом порядке, при котором сначала выводится корень, а потом значение левого и правого поддеревьев (для уже рассматривавшегося дерева это дает последовательность значений 4, 2,1,3,7,5), и обход в обратном порядке, при котором сначала выводятся значения узлов левого и правого поддеревьев, а затем — корня (для нашего дерева это дает последовательность 1, 3, 2, 5, 7,4).
Псевдокоды описанных обходов дерева очень просты. Алгоритм процедуры симметричного обхода представлен на рис. 14.25.
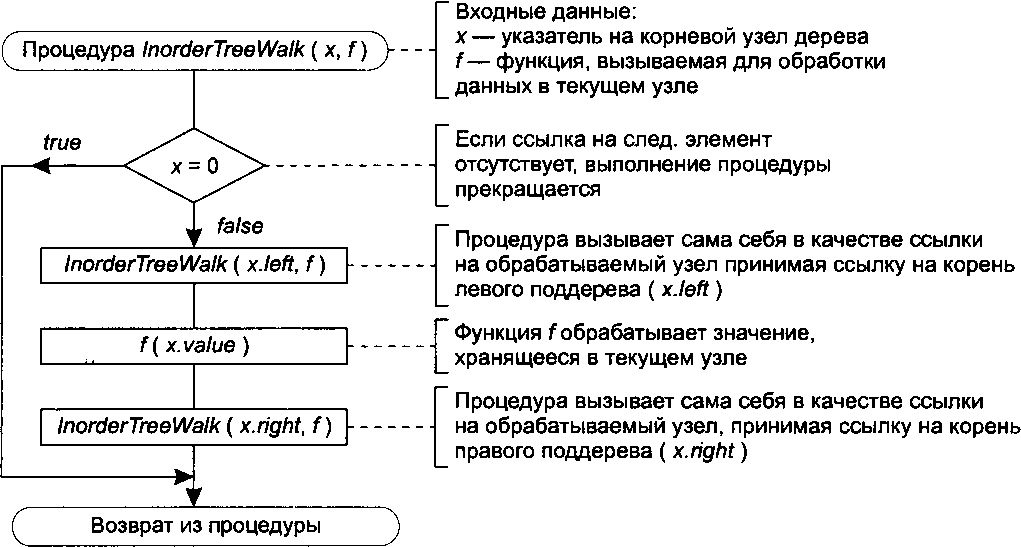 Рис. 14.25. Процедура симметричного обхода бинарного дерева
Рис. 14.25. Процедура симметричного обхода бинарного дерева
|
В этой процедуре для обхода всех узлов дерева и выполнения над ними определенных операций используется рекурсия.
Рекурсия часто применяется в алгоритмах обработки разного рода сложно структурированных объектов, в частности документов в формате XML, когда количество дочерних узлов и уровень их вложенности заранее не известны.

|
Основные операции при работе с бинарным деревом поиска — поиск в нем определенного значения, а также поиск наименьшего и наибольшего элементов дерева и поиск предшествующего и последующего элементов для данного.
Выполнение операции поиска основано на том, что находясь на определенной вершине, всегда можно однозначно указать, в каком из поддеревьев находится искомое значение (если таковое имеется в данном дереве), так как согласно свойству бинарного дерева поиска все значения узлов в левом поддереве не больше, а в правом — не меньше значения в корне.
Что касается поиска наименьшего и наибольшего элементов в бинарном дереве поиска, то из свойства бинарного дерева поиска очевидно: чтобы достичь наименьшего (наибольшего) элемента, надо двигаться по левым (или, соответственно, правым) ветвям дерева до тех пор, пока это возможно.
14.4.7. Представление и обработка данных в виде графов
Графы формально описывают множество близких ситуаций. Самым привычным примером служит карта автодорог, на которой изображены перекрестки и связывающие их дороги. Перекрестки являются вершинами графа, а дороги — его ребрами. Графы могут быть ориентированы (подобно улицам с односторонним движением) или взвешены, когда каждой дороге приписана стоимость путешествия по ней (если, например, дороги платные).
С формальной точки зрения граф представляет собой упорядоченную пару множеств G = ( Vf Е), первое из которых состоит из вершин {узлов) графа, а второе — из его ребер. Ребро связывает между собой две вершины. При работе с графами часто решается вопрос, как проложить путь из ребер от одной вершины графа к другой. В этом случае говорят о движении по ребру, что означает переход из вершины А графа в другую вершину B1 связанную с ней ребром AB (ребро графа, связывающее две вершины, для краткости обозначается этой парой вершин). В этом случае говорят, что ребро А примыкает к ребру В или что эти две вершины соседние.
Граф может быть ориентированным или нет. Ребра неориентированного графа, чаще всего называемого просто графом, можно проходить в обоих направлениях (рис. 14.26). В этом случае ребро — это неупорядоченная пара вершин, его концов.
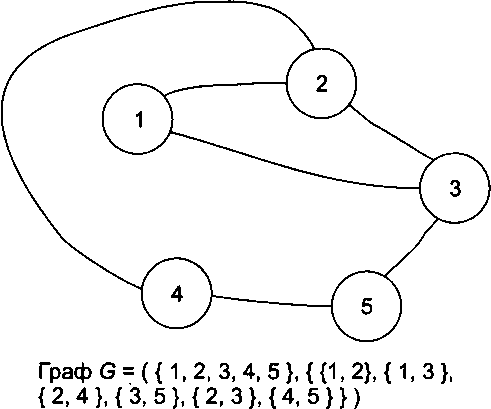 Рис. 14.26. Неориентированный граф
Рис. 14.26. Неориентированный граф
|
В ориентированном графе, или орграфе, ребра представляют собой упорядоченные пары вершин: первая вершина — это начало ребра, вторая — его конец (рис. 14.27).
Полный граф — это граф, в котором каждая вершина соединена со всеми остальными. Количество ребер в полном графе без петель с N вершинами равно (N2 - N)/2. В полном ориентированном графе разрешается переход из любой вершины в любую другую. Поскольку в графе переход по ребру разрешается в обоих направ-
Подграф (VsfEs) графа или орграфа (VyE) состоит из некоторого подмножества вершин, Vs С Vy и некоторого подмножества ребер, их соединяющих, Es С Е.
Путь в графе или орграфе — это последовательность ребер, по которым можно поочередно проходить. Другими словами, путь из вершины А в вершину В начинается в Л и проходит по набору ребер до тех пор, пока не будет достигнута вершина В. С формальной точки зрения путь из вершины Vx в вершину Vy — это последовательность ребер графа:
vxvx+l> vx+\vx+2> ••• vy-\vy
Необходимо, чтобы любая вершина встречалась на таком пути не более, чем однажды. У всякого пути есть длина — количество ребер в нем. Длина пути ABy BCy CDy DE равна 4.
Граф или орграф называется связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл — это путь, который начинается и кончается в одной и той же вершине. В ациклическом графе или орграфе циклы отсутствуют. Связный ациклический граф называется неукорененным деревом. Структура неуко- рененного дерева такая же, как и у дерева, только в нем не выделен корень. Однако каждая вершина неукорененного дерева может служить его корнем.
| лениях, а переход по ребру в орграфе — только в одном, в полном орграфе в два раза больше ребер, то есть их количество равно N[7] - N. |
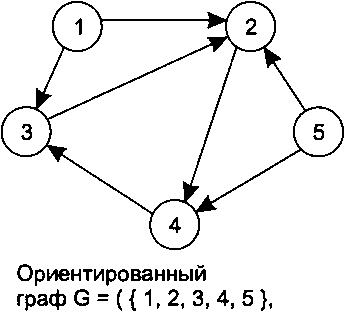 {(1,2),(1,3),(2,4),(3,2), (4,3),(5,2),(5,4)})
Рис. 14.27. Ориентированный граф
{(1,2),(1,3),(2,4),(3,2), (4,3),(5,2),(5,4)})
Рис. 14.27. Ориентированный граф
|
Информацию о графах или орграфах в пригодном для обработки компьютерными алгоритмами виде можно хранить двумя способами: в виде матрицы примыканий и в виде списка примыканий\
Матрица примыканий обеспечивает быстрый доступ к информации о ребрах графа, однако, если в графе мало ребер, эта матрица будет содержать гораздо больше пустых клеток, чем заполненных. Длина списка примыканий пропорциональна числу ребер в графе, однако при пользовании списком время получения информации о ребре увеличивается.
Матрица примыканий ConMat графа G = (V7E) с числом вершин |V| = Nзаписывается в виде двухмерного массива размером NxN. В каждой ячейке [у] этого массива записано значение 0 за исключением лишь тех случаев, когда из вершины Vi в вершину Vj ведет ребро, и тогда в ячейке записано значение 1:
| I |
I, если [ViVj^e E
для всех г и j от 1 до N.
О, если [VlVjfe E
На рис. 14.28 изображены матрицы примыканий для графа и орграфа, изображенных на рис. 14.26 и 14.27.
12345 12345
| .0 | 0. | .0 | 0. |
| Рис. 14.28. Матрицы примыканий графа и орграфа |
Список примыканий ConList графа G = (V1E) с числом вершин |V| = Nзаписывается в виде одномерного массива длины N1 каждый элемент которого представляет собой ссылку на список. Такой список приписан каждой вершине графа и содержит по одному элементу на каждую вершину графа, соседнюю с данной.
На рис. 14.29 изображен список примыканий для орграфа, изображенного на рис. 14.27. На этом рисунке буквами Lvn обозначены вершины графа, а буквами vN — те вершины, к которым направлены выходящие из данной вершины ребра.
Ln'. V2, V3; Ly2- V4I Lv3: V2l Lv4. V3; Lyb'. v2l V4;
Рис. 14.29. Список примыканий для орграфа
При работе с графами часто приходится выполнять некоторое действие по одному разу с каждой из вершин графа, например, когда некоторую порцию информации следует передать каждому из компьютеров в сети. При этом нерационально посещать какой-либо компьютер дважды. Аналогичная ситуация возникает, если нужно собирать, а не распространять информацию.
Подобный обход можно совершать двумя способами. При обходе в глубину проход по выбранному пути осуществляется настолько глубоко, насколько это возможно, а при обходе по уровням происходит равномерное движение вдоль всех возможных направлений.
Обход в глубину
При обходе в глубину происходит посещение первого узла, а затем передвижение вдоль ребер графа, пока не будет достигнут тупик. Узел неориентированного графа является тупиком, если уже посещены все примыкающие к нему узлы. В ориентированном графе тупиком также оказывается узел, из которого нет выходящих ребер.
После попадания в тупик следует вернуться назад вдоль пройденного пути, пока не будет обнаружена вершина, у которой есть еще не посещенный сосед, а затем двигаться в новом направлении. Процесс оказывается завершенным после того, как произошел возврат в отправную точку, а все примыкающие к ней вершины уже посещены (рис. 14.30).
При реализации алгоритма обхода в глубину используется рекурсивный вызов процедуры.
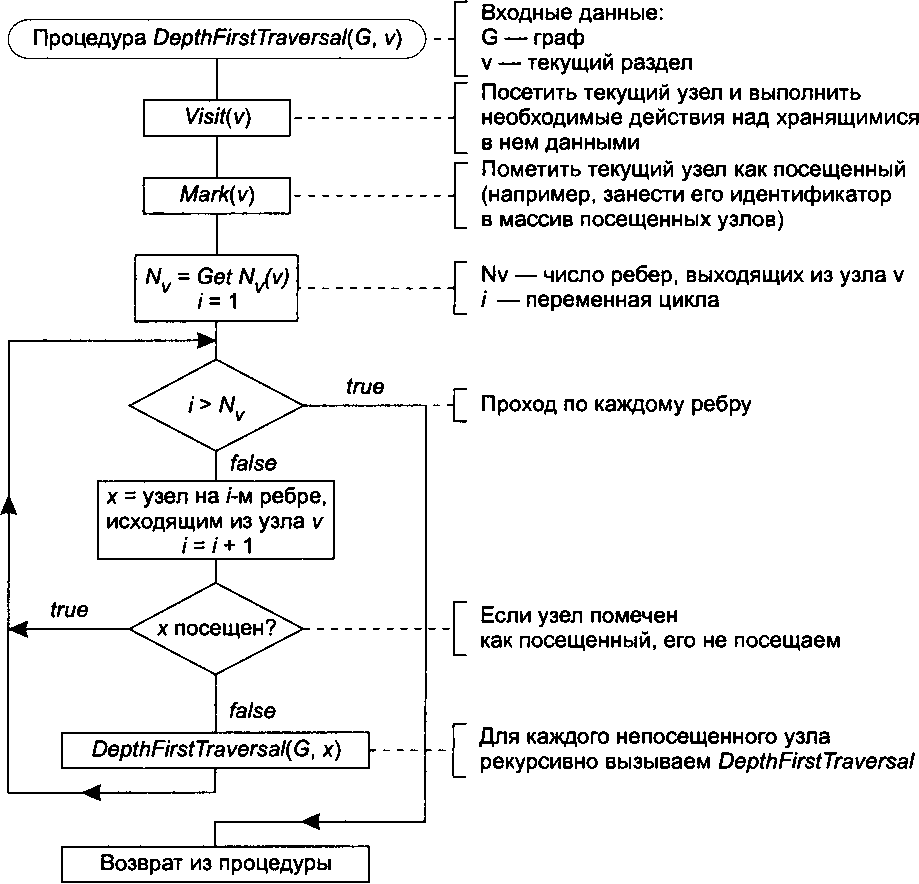 Рис. 14.30. Рекурсивная процедура обхода графа в глубину
Рис. 14.30. Рекурсивная процедура обхода графа в глубину
|
Обход по уровням
При обходе графа по уровням после посещения первого узла происходит обход всех соседних с ним вершин. При втором проходе посещаются все вершины
на расстоянии «двух ребер» от начальной. При каждом новом проходе обходятся вершины, расстояние от которых до начальной на единицу больше предыдущего. В графе могут быть циклы, поэтому не исключено, что одну и ту же вершину можно соединить с начальной двумя различными путями. При обходе этой вершины впервые проходится самый короткий до нее путь, и посещать ее второй раз нет необходимости. Поэтому, чтобы предупредить повторное посещение, приходится либо вести список посещенных вершин, либо сопоставить каждой вершине флажок, указывающий, посещена она или нет.
Входные данные: G — граф
|
| Извлечь из начала очереди узел х |
| Для каждого непосещенного узла: посещение и обработка; пометка как посещенного; помещение в конец очереди |
| ( Возврат из процедуры^) |
V — текущий раздел Посетить текущий раздел и выполнить необходимые действия над хранящимися в нем данными
| - Поместить текущий узел в конец очереди |
| - Проход по каждому ребру |
| ^посешен^Ъ>________ -Г Если узел помечен как посещенный, его не по |
| посещаем |
Пометить текущий узел как посещенный (например, занести его идентификатор в массив посещенных узлов)
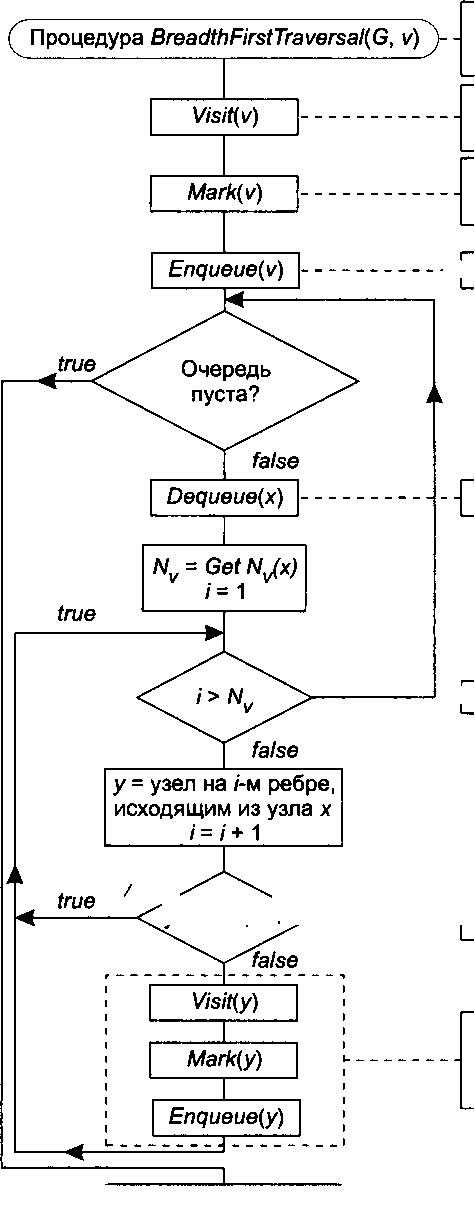
Рис. 14.31. Обход графа по уровням
Алгоритм обхода вершин графа по уровням приведен на рис. 14.31. В отличие от обхода в глубину, этот алгоритм реализован с использованием очереди. Очередь — это специальный программный механизм, предназначенный для упорядоченного хранения и извлечения данных. При помощи процедуры Enqueue заданный объект помещается в конец очереди, а процедура Dequeue извлекает из начала очереди размещенный там объект. Таким образом, пока идет обработка данных в узлах текущего уровня, узлы следующего уровня, связанные ребрами с текущими узлами, помещаются в очередь.
При анализе графов и применении их для решения различных информационных задач используют стандартные алгоритмы поиска минимального пути, поиска пути с минимальным (максимальным) весом ребер, анализа компонентов двусвязности.
Дата добавления: 2016-04-14; просмотров: 3809;
