Зависимость между моментом силы относительно оси и моментом силы относительно точки, которая лежит на этой оси

Установим зависимость между моментом силы 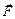относительно точки О (рис. 6.6) и моментом этой силы относительно оси Оz.

Рисунок 6.6

Раньше, (формула (6.1)) мы получили, что модуль момента силы относительно точки О равен двум площадям треугольника ОАВ. Нетрудно убедиться, что момент силы 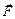относительно оси Оz равен двум площадям треугольника ОА1В1. Как известно из школьного курса геометрии, площадь проекции треугольника ОАВ на плоскость І равна площади треугольника ОАВ, умноженной на косинус угла между плоскостями, в которых находятся эти треугольники .

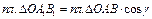Помножим обе части этого равенства на два, получим:

,

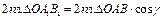то есть

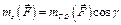
(6.9)

Вывод.

Если поменять точку, то есть рассмотреть момент силы относительно другой точки, т. О₁, это уже будет другой треугольник О₁АВ. Но проекция его на плоскость І будет такая же – ΔОА₁В₁, то есть формула (6.9) имеет место для произвольной точки, которая принадлежит оси Оz. Раньше (формулы 6.6), мы получили проекции момента силы относительно точки О на координатные оси Ох, Оу, Оz. Сравнивая формулы (6.6) и (6.9), получим аналитические формулы для определения моментов силы относительно координатных осей, а именно:

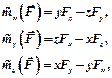(6.10)

где: x, y, z - координаты точки, в которой приложена сила;

Fx, Fy, Fz - проекции вектора силы на оси координат.

6.5 Возможные случаи приведения системы сил, произвольно расположенных в пространстве. Инварианты «Статики»

Согласно основной теореме статики (тема 4), в общем случае система сил 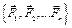, произвольно расположенных в пространстве, может быть заменена одной силой, главным вектором , и одной парой сил, момент которой равен главному моменту относительно центра приведения (точки О) .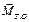

Возможны частные случаи приведения пространственной системы сил к заданному центру.

Случай 1. система сил приводится к паре сил, момент которой равен главному моменту. В этом случае главные моменты системы сил относительно всех точек пространства геометрически равны.

Случай 2. система сил приводится к равнодействующей, которая проходит через точку О (центр приведения).

Случай 3. . Покажем, что в этом случае систему можно привести к одной силе, а значит, равнодействующей.

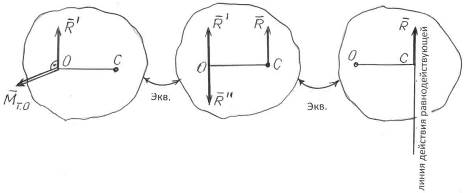
Имеем силу , приложенную в точке О и пару сил с моментом , который перпендикулярен силе (рис. 6.7 а).

а б в

Рисунок 6.7.

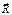Изобразим пару сил, момент которой известен, , двумя силами: одну силу приложим в точке О (рис. 6.7 б) и направим противоположно силе , вторую силу пары приложим в точке С параллельно на расстоянии . Модули всех трех сил одинаковые 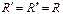. Таким образом, вместо силы и пары 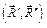получим одну силу 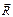(рис. 6.7 в), потому что

.

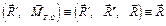В этом случае система сил приводится к равнодействующей, которая приложена в точке С на расстоянии

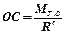(6.11)

от «старого» центра приведения, точки О.

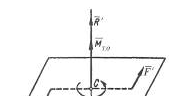Случай 4. параллельна 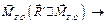динама. В этом случае пара, момент которой равен главному моменту, расположена в плоскости перпендикулярной главному вектору, изобразим её силами 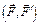(рис. 6.8), тогда .

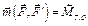Совокупность силы 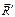и пары сил (с моментом ), которая расположена в плоскости, перпендикулярной линии действия силы 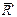, называют силовым винтом или динамой.

Название силовой винт объясняется движением по винтовой линии под действием такой совокупности .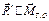

Случай 5. 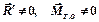, главный вектор и главный момент образуют угол α (α ≠ 0, α ≠ 90о, α ≠ 180о).   Это наиболее общий случай приведения произвольной системы сил к центру (рис. 6.9). Покажем, что в этом случае система сил приводится к силовому винту (динаме).

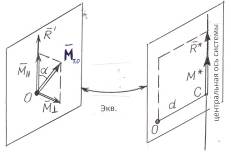Рисунок 6.9

Для этого момент пары разложен на две взаимно перпендикулярные составляющие

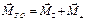. (6.12)

Величины этих составляющих такие:

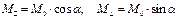, (6.13)

их направления: 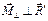. С вектором 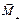и силой 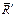поступим так же, как в случае 3. То есть, получим силу 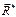, которая приложена в точке С на расстоянии

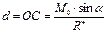. (6.14)

Пару сил с моментом 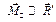(учитывая то, что момент пары является свободным вектором) приложим в этой же точке С и обозначим . Получим, как в случае 4, силовой винт (динаму). Прямая, по которой действует сила динамы, называется центральной осью системы.

Силовой винт называют правым, если направления 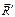и совпадают и левым, если угол между 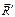и равен 180^о.

 

Таким образом, в этом случае система сил приводится к силовому винту, центральная ось которого параллельна главному вектору и расположена от точки С на расстоянии d (формула (6.14)).Можно доказать, что момент пары динамы равен наименьшему значению главного момента системы сил (Дополнение Д).

Случай 6. . Это особенный случай - случай уравновешенной системы сил. Рассмотрим его в следующем параграфе.

 

Инварианты раздела «Статика»

 

Величины, которые не изменяются при определенных превращениях, называются инвариантами относительно данных превращений.

 

В разделе «Статика» такими являются величины, которые не зависят от выбора центра приведения.

Первым векторным инвариантом статики является главный вектор системы сил, потому что геометрическая сумма одной и той же системы сил не зависит от точки, в которую переносятся эти силы (тема 4).

Сравним главные моменты системы сил относительно двух центров приведения (точки О₁ и точки О₂, рис. 6.10). Для этого надо рассмотреть моменты одной из сил системы (к = 1, 2, …, n) относительно точек_. О₁ и О_2.. Согласно формуле (6.2)

, .

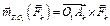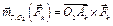Учитывая, что 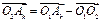имеем, умножив левую и правую части этого равенства на ,

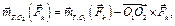(6.15)

где 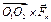– момент силы , которая при-

ложена в точке О₂, относительно точки О₁ .

Если сложить все левые части и все правые части формул (6.15), приняв k = 1, 2, ..., n, получим формулу (6.16).

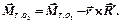(6.16)

При изменении центра приведения главный момент системы сил уменьшается на момент главного вектора, который приложен в новом центре приведения относительно старого центра.

 

Скалярно умножив векторное равенство (6.16) на главный вектор 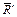и учитывая, что смешанное произведение 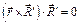, имеем

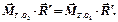(6.17)

Скалярное произведение главного вектора на главный момент не зависит от центра приведения, то есть является вторым инвариантом произвольной системы сил.

 

Составим таблицу всех возможных случаев приведения произвольной пространственной системы сил к более простому виду (табл. 6.1).

 

Таблица 6.1 – Случаи приведения пространственной системы сил к более простому виду

Номер позиции	Значение	Результат приведения
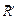
Главного вектора	Главного момента	Второго инварианта
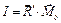
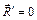
				Пара сил
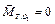
				Равнодействующая в точке О
				Равнодействующая в точке С,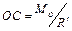
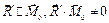
				Динама с осью в точке О
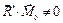
				Динама с осью в точке С
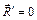
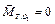
				Система сил уравновешенная