Уравнения равновесия пространственной системы сил
Выше (6.5, случай 6) было установлено, что
| Геометрической формой условия равновесия произвольной пространственной системы сил является равенство нулю ее главного вектора и главного момента |
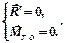 (6.18)
(6.18)
Учитывая, что 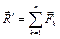 ,
,  , спроектируем формулы (6.18) на Декартовы оси координат. Имеем аналитическую форму уравнений равновесия произвольной пространственной системы сил:
, спроектируем формулы (6.18) на Декартовы оси координат. Имеем аналитическую форму уравнений равновесия произвольной пространственной системы сил:


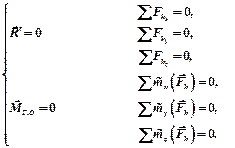 (6.19)
(6.19)
Последние три уравнения имеют место из-за того, что проекция момента силы относительно точки на ось, которая проходит через эту точку, равна моменту силы относительно оси (формула (6.9)).
| Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на три координатные оси и суммы моментов всех сил системы относительно этих координатных осей равнялись нулю. |
Вывод. При решении задач на равновесие произвольной пространственной системы сил, которая приложена к твердому телу, мы должны составить шесть уравнений равновесия (6.19), потому имеем возможность с помощью этих уравнений определить шесть неизвестных величин.
Рассмотрим случай пространственной системы параллельных сил. Систему координат выберем так, чтобы ось Оz была параллельна линиям действия сил (рис. 6.11).
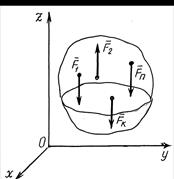 Рисунок 6.11
Рисунок 6.11
|
Если система сил находится в равновесии, то имеют место уравнения (6.19). Система сил, показана на рис. 6.11, является упрощенным вариантом произвольной пространственной системы сил, потому и уравнения (6.19) должны упроститься. Выясним, какие из уравнений (6.19) в данном случае выполняются тождественно, то есть является лишними. Такими является:
– суммы проекций сил на оси Оx и Оy, потому что силы 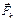 им перпендикулярны;
– сумма моментов сил относительно оси Оz, потому что силы им перпендикулярны;
– сумма моментов сил относительно оси Оz, потому что силы 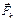 параллельны ей
(п. 6.3. Рекомендации для практического занятия). параллельны ей
(п. 6.3. Рекомендации для практического занятия).
|
Таким образом, остались три уравнения:
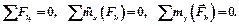 (6.20)
(6.20)
| Для равновесия параллельной пространственной системы сил необходимо и достаточно, чтобы: – сумма проекций сил системы на ось параллельную силам равнялась нулю; – суммы моментов сил системы относительно двух других осей равнялись нулю. |
Вывод. При решении задач на равновесие параллельной пространственной системы сил, которая приложена к твердому телу, мы должны составить три уравнения равновесия и имеем возможность с помощью этих уравнений определить три неизвестных величины.
На первой лекции по разделу «Статика» мы выяснили, что имеют место шесть разновидностей систем сил, которые могут встретиться в Вашей практике инженерных расчетов. Кроме того есть две возможности расположения пар сил : в пространстве и в плоскости. Сведем все уравнения равновесия для сил и для пар сил в одну таблицу (табл. 6.2), в которой в последней колонке отметим количество неизвестных величин, которые позволит определить система уравнений равновесия.
Таблица 6.2 – Уравнения равновесия разных систем сил
| Вид системы сил | Уравнения равновесия | Количество определяемых неизвестных | |
Сходящаяся плоская
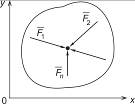
| 
| ||
Параллельная плоская
(  оси 0у) оси 0у)

| 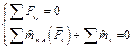 т. А – произвольная,
принадлежащая
плоскости 0ху
т. А – произвольная,
принадлежащая
плоскости 0ху
| ||
Произвольная плоская
(в плоскости 0ху)

| 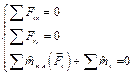 т. А – произвольная,
принадлежащая
плоскости 0ху
т. А – произвольная,
принадлежащая
плоскости 0ху
|
Продолжение таблицы 6.2
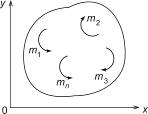
Система пар
в плоскости
| 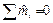
| ||
Сходящаяся пространственная
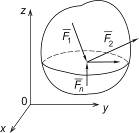
| 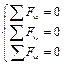
| ||
Параллельная пространственная
( 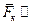 оси 0z) оси 0z)
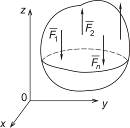
| 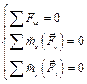
|
Продолжение таблицы 6.2
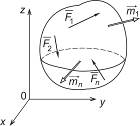
Произвольная пространственная
| 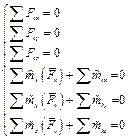
| ||
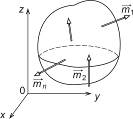
Система пар в пространстве
| 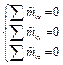
|
Вопросы для самоконтроля по теме 6
1. Как найти момент силы относительно оси?
2. Какая зависимость существует между моментом силы относительно точки и моментом этой же силы относительно оси, которая проходит через эту точку?
3. В каких случаях момент силы относительно оси равен нулю? А когда он наибольший?
4. В каких случаях система сил приводится к равнодействующей?
5. В каком случае пространственная система сил приводится:
– к паре сил;
– к динамическому винту?
6. Что называется инвариантом статики? Какие Вы знаете инварианты статики?
7. Запишите уравнения равновесия произвольной пространственной системы сил.
8. Сформулируйте необходимое и достаточное условие равновесия параллельной пространственной системы сил.
9. Изменится ли главный вектор системы сил при изменении центра приведения? А главный момент?
Тема 7. ФЕРМЫ. ОПРЕДЕЛЕНИЕ УСИЛИЙ
Дата добавления: 2016-03-15; просмотров: 11593;
