Будем считать, что стержни растянуты, то есть реакция стержня на узел направлена от узла.
Если объект изучения – узел А, имеем такую схему сил (рис. 7.6).
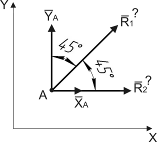 Рисунок 7.6
Рисунок 7.6
| Дано: УА = 60 кН, ХА = 20 кН;.
Определить R1, R2.
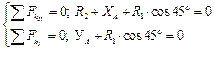 .
Решаем эти уравнения относительно R1 и R2. .
Решаем эти уравнения относительно R1 и R2.
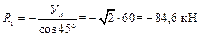 , ,
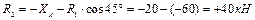 . .
|
Полученные знаки в ответах свидетельствуют о том, что направление R2 выбрано верно, стержень 2 – растянут; направление R1 выбрано неверно, стержень 1 – сжат.
Проверку выполним, применив геометрическую форму условий равновесия сходящейся плоской системы сил. Выберем масштаб 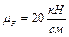 и начнем строить силовой четырехугольник (т. к. четыре силы действуют на свободный узел А) из точки О, отложив известную силу, например
и начнем строить силовой четырехугольник (т. к. четыре силы действуют на свободный узел А) из точки О, отложив известную силу, например 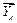 ( рис. 7.7 а). Потом в конец силы
( рис. 7.7 а). Потом в конец силы 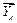 прикладываем силу
прикладываем силу 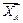 . Через конец
. Через конец 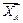 проведем линию действия силы
проведем линию действия силы 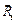 , а из начала силы
, а из начала силы 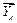 линию действия силы
линию действия силы 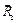 (I вариант).
(I вариант).
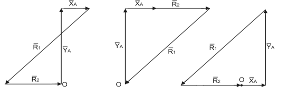
| ||
| а | б Рисунок 7.7 | в |
Можно второй вариант: из точки О построить 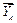 (рис. 7.7 б), в ее конец приложить
(рис. 7.7 б), в ее конец приложить 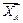 , через конец силы
, через конец силы 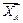 провести линию параллельную линии действия силы
провести линию параллельную линии действия силы 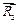 , а из начала силы
, а из начала силы 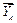 линию параллельную силе
линию параллельную силе 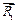 . Есть еще третий вариант: из точки О построить силу
. Есть еще третий вариант: из точки О построить силу 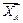 , в конце
, в конце 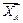 построить силу
построить силу 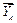 , потом провести линию параллельную силе
, потом провести линию параллельную силе 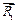 , а с начала силы
, а с начала силы 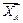 линию, параллельную силе
линию, параллельную силе 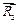 (рис. 7.7 в).
(рис. 7.7 в).
Измеряя длины векторов, которые изображают силы 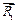 и
и 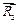 , получаем их величины: длина
, получаем их величины: длина 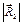 = 2 см, то есть
= 2 см, то есть 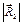 = 40 кН, длина
= 40 кН, длина 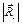 = 4,23 см, то есть
= 4,23 см, то есть
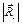 = 84,6 кН (потому что масштаб
= 84,6 кН (потому что масштаб 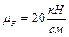 ).
).
Направления векторов 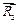 и
и 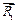 в силовых многоугольниках совпали с ответами, которые мы получили аналитическим способом: стержень 1 – сжат (знак «–» в ответе, стержень 2 – растянут, знак «+» в ответе).
в силовых многоугольниках совпали с ответами, которые мы получили аналитическим способом: стержень 1 – сжат (знак «–» в ответе, стержень 2 – растянут, знак «+» в ответе).
Следующим будет узел С, потому что реакцию стержня 1 мы уже знаем, а реакции 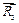 и
и 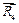 – две неизвестные. Принимая во внимание то, что стержень 1 - сжат будем на рис. 7.8 а показывать реакцию
– две неизвестные. Принимая во внимание то, что стержень 1 - сжат будем на рис. 7.8 а показывать реакцию 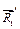 направленную к узлу С. Опять составляем уравнения равновесия сходящейся плоской системы сил, действующих на узел С.
направленную к узлу С. Опять составляем уравнения равновесия сходящейся плоской системы сил, действующих на узел С.
Дано: 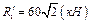 . Найти
. Найти 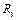 и
и 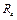 .
.
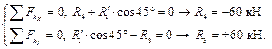

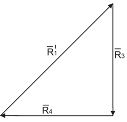
а б
Рисунок 7.8
Строим в выбранном раньше масштабе силовой треугольник, начиная с известной силы 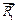 , с конца ее проводим линию параллельную, например, силе
, с конца ее проводим линию параллельную, например, силе 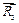 , а из начала вектора
, а из начала вектора 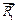 – линию параллельную
– линию параллельную 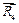 (рис. 7.8 б). Стрелки в силовом треугольнике в одном направлении (как будто вода по трубе течет). Имеем: стержень 4 – сжат, стержень 3 – растянут. Длина
(рис. 7.8 б). Стрелки в силовом треугольнике в одном направлении (как будто вода по трубе течет). Имеем: стержень 4 – сжат, стержень 3 – растянут. Длина 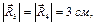 поэтому величины R3 = R4 = 60 кН. Ответы совпали с результатом аналитического решения.
поэтому величины R3 = R4 = 60 кН. Ответы совпали с результатом аналитического решения.
После этого можно рассмотреть равновесие какого узла? D – невозможно, потому что три неизвестных реакции 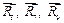 , а к узлу Е приложены две известные реакции
, а к узлу Е приложены две известные реакции 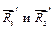 , и две неизвестные –
, и две неизвестные – 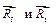 .
.
Схема сил, с учетом знаков 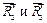 , которые действуют на узел Е, изображена на рисунке 7.9.
, которые действуют на узел Е, изображена на рисунке 7.9.
Дано: 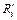 = 60 кН; = 60 кН; 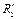 = 40 кН; Р1= 20 кН.
Найти: R5, R6.
Опять составляем два уравнения равновесия и строим силовой пятиугольник, начиная с известной силы (можно с = 40 кН; Р1= 20 кН.
Найти: R5, R6.
Опять составляем два уравнения равновесия и строим силовой пятиугольник, начиная с известной силы (можно с 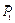 , или с , или с 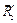 , или с , или с 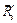 ). Масштаб тот же. После узла Е можно рассматривать узел F, или узел D. Узел В будет проверочным, потому что все усилия уже известны. ). Масштаб тот же. После узла Е можно рассматривать узел F, или узел D. Узел В будет проверочным, потому что все усилия уже известны.
| 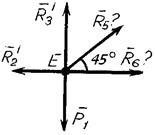 Рисунок 7.9
Рисунок 7.9
|
Таким образом, рассмотрев равновесие всех k узлов (шести в этом примере), составим 2k уравнений равновесия, из которых можно получить 2k неизвестных. Последний узел будет проверкой, т. к. все величины реакций стержней уже найдены.
3) Определение усилий в стержнях методом Риттера
Метод Риттера заключается в том, что ферму условно перерезают на две части по тем стержням, усилия в которых надо определить. Из-за того, что система сил, которые действуют на каждую часть фермы, – плоская произвольная, можно составлять три уравнения равновесия в форме (5.5) или (5.6), или (5.7), а значит, можно найти три неизвестные реакции стержней. То есть, рассекать (перерезать) ферму можно в том месте, где будет три стержня, потому что неизвестных должно быть не больше трех.
Для рассматриваемого примера первый разрез І–І можно сделать по стержням 4, 5, 6 (рис. 7.4). Потом левую (или правую) часть фермы «отбросить» и рассматривать равновесие правой (или левой) части. Опять считаем, что стержни растянуты, потому реакции стержней 4, 5, 6 направляем от узлов (рис. 7.10).
Имеем: Дано Р2 = 20 кН; RB = 20 кН. Определить R4, R5, R6.
Составляем уравнения равновесия. Для того, чтобы в каждом уравнении была одна неизвестная величина, чаще всего составляют уравнения с помощью формул (5.6) или (5.7).
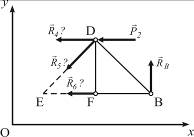 Рисунок 7.10
Рисунок 7.10
| Центрами моментов в уравнениях равновесия выбираем точки пересечения неизвестных (точка D и точка Е). |
Силы 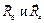 параллельны, потому нет точки их пересечения. Составляем уравнение проекций сил на ось, перпендикулярную этим векторам.
параллельны, потому нет точки их пересечения. Составляем уравнение проекций сил на ось, перпендикулярную этим векторам.
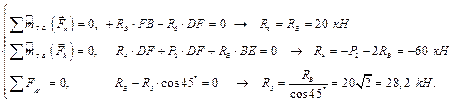
 Способом Риттера можно определить усилия в стержнях 6, 7, 9; выполнив разрез ІІ–ІІ по этим стержням (рис. 7.4). «Отбросим» верхнюю часть, рассмотрим равновесие нижней части, а именно стержня FB фермы (рис. 7.11).
Способом Риттера можно определить усилия в стержнях 6, 7, 9; выполнив разрез ІІ–ІІ по этим стержням (рис. 7.4). «Отбросим» верхнюю часть, рассмотрим равновесие нижней части, а именно стержня FB фермы (рис. 7.11).
Дано: RB=20 кН. Определить R6, R7, R9.
Составим уравнения равновесия в форме трех моментов (формула (5.6)). За центры моментов берем точки пересечения неизвестных – точки D, F и B.
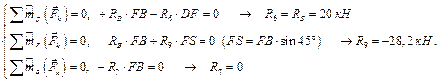
После того, как усилия в стержнях найдены двумя способами, убедимся, что ответы совпадают. Ответы усилий в стержнях заносятся в таблицу с указанием знаков «+» – стержень растянут, а «–» – стержень сжат.
Выводы:
1. Способом Риттера удается определить реакцию стержня избирательно, независимо от усилий в других стержнях.
2. В способе вырезания узлов после того, как усилия в стержнях найдены с помощью аналитических уравнений, делается проверка путем построения силовых многоугольников.
3. Если в узле сходятся три стержня, из которых два расположены по одной прямой, и на этот узел не действует внешняя сила, то усилие в третьем стержне равняется нулю (стержень № 7 в рассмотренном примере).
4. Если в ненагруженном узле сходятся два стержня, то усилия в этих стержнях равны нулю.
Вопросы для самоконтроля по теме 7
1. Какие конструкции называют фермами?
2. Какая зависимость существует между количеством стержней и количеством узлов фермы?
3. Какие допущения принимаются для фермы относительно стержней?
4. Какая последовательность действий при определении реакций связей фермы?
5. Какая последовательность действий в способе вырезания узлов при определении усилий в стержнях?
6. Какая последовательность действий в способе Риттера? В чем целесообразность этого метода определения усилий в стержнях?
Тема 8. ТРЕНИЕ
| Трением называют сопротивление возможному или действительному перемещению контактирующих тел, которое возникает при их контакте. |
По кинематическим признакам различают трение скольжения (пример - трение подошв человека о землю) и трение качения (пример - колесо вагона по рельсам). Исследованием этого важного явления занимались Леонардо да Винчи, французские физики Амонтон и Кулон [1, 2].
Законы Кулона
Шарль Кулон в 1781 г. установил основные законы для сухого трения при покое. Данные законы справедливы, когда поверхности тел не вдавливаются друг в друга и их шероховатость не очень большая. Данные законы легко установить с помощью эксперимента, который можно выполнить на приборе, который называется «Трибометром» (рис. 8.1).
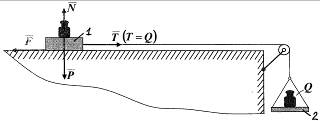
Рисунок 8.1
Если к телу 1, что находится на шероховатой поверхности, приложить горизонтальную силу 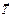 , то действие этой силы вызовет появление силы сцепления
, то действие этой силы вызовет появление силы сцепления 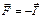 , которая не дает телу 1 двигаться. Есть возможность увеличивать силу
, которая не дает телу 1 двигаться. Есть возможность увеличивать силу 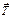 , добавляя гирьки на платформе 2. Тело 1 будет оставаться в покое, пока модуль силы
, добавляя гирьки на платформе 2. Тело 1 будет оставаться в покое, пока модуль силы 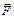 не достигнет значения
не достигнет значения 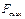 .То есть получим, что сила
.То есть получим, что сила 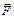 меняется от нуля до
меняется от нуля до 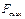 .
.
Первый закон.
Сила трения скольжения находится в общей касательной плоскости контактирующих поверхностей и направлена противоположно возможному движению тела под действием активных сил. Сила трения зависит от активных сил и ее модуль находится между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, то есть 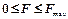 . (8.1) . (8.1)
|
Второй закон.
| Максимальная сила трения (при других одинаковых условиях) не зависит от величины площади контактирующих поверхностей. |
Из данного закона выплывает, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью ее положить, широкой или узкой.
Третий закон.
| Максимальная сила трения сцепления (сила скольжения) прямо пропорциональная силе нормального давления (нормальной реакции), то есть |
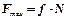 , (8.2)
, (8.2)
где безразмерный коэффициент f называют коэффициентом трения скольжения.
Четвертый закон.
| Коэффициент трения скольжения зависит от материала и физического состояния контактирующих поверхностей (величины и характера шероховатости, влажности, температуры и другое). |
В таблице 8.1 приведены коэффициенты трения скольжения для некоторых материалов.
Таблица 8.1 – Коэффициент трения скольжения для некоторых материалов
| Материал | Коэффициент трения скольжения |
| Сталь о лед | 0,015 |
| Сталь о сталь | 0,150 |
| Бронза о чугун | 0,200 |
| Железо о железо | 1,000 |
| Дуб о дуб вдоль волокон | 0,620 |
| Дуб о дуб поперек волокон | 0,540 |
| Кирпич о бетон | 0,760 |
Пятый закон.
| Коэффициент трения скольжения зависит от относительной скорости скольжения. |
Для большинства материалов эта зависимость изображена на рис. 8.2, из которой видно, чтокоэффициент трения при движении меньше коэффициента статического трения f с.Считают, что коэффициент трения скольжения равняется0,9 fстатического.

Рисунок. 8.2
Дата добавления: 2016-03-15; просмотров: 1687;
