Влияние способа закрепления концов стержня.
Формула Эйлера была получена путем интегрирования приближенного дифференциального уравнения изогнутой оси стержня при определенном закреплении его концов (шарнирно-опертых). Значит, найденное выражение критической силы справедливо лишь для стержня с шарнирно-опертыми концами и изменится при изменении условий закрепления концов стержня.
Закрепление сжатого стержня с шарнирно-опертыми концами мы будем называть основным случаем закрепления. Другие виды закрепления будем приводить' к основному случаю.
Если повторить весь ход вывода для стержня, жестко защемленного одним концом и нагруженного осевой сжимающей силой на другом конце (Рис.2), то мы получим другое выражение для критической силы, а следовательно, и для критических напряжений.
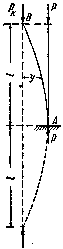
Рис.2. Расчетная схема стержня с жесткозакрепленным одним концом.
Предоставляя право студентам проделать это во всех подробностях самостоятельно, подойдем к выяснению критической силы для этого случая путем следующих простых рассуждений.
Пусть при достижении силой Р критического значения колонна будет сохранять равновесие при слабом выпучивании по кривой АВ. Сравнивая два варианта изгиба видим, что изогнутая ось стержня, защемленного одним концом, находится совершенно в тех же условиях, что и верхняя часть стержня двойной длины с шарнирно-закрепленными концами.
Значит, критическая сила для стойки длиной 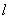 с одним защемленным, а другим свободным концами будет та,же, что для стойки с шарнирно-опертыми концами при длине
с одним защемленным, а другим свободным концами будет та,же, что для стойки с шарнирно-опертыми концами при длине 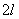 :
:
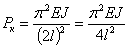
Если мы обратимся к случаю стойки, у которой оба конца защемлены и не могут поворачиваться (Рис.3), то заметим, что при выпучивании, по симметрии, средняя часть стержня, длиной 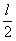 , будет работать в тех же условиях, что и стержень при шарнирно-опертых концах (так как в точках перегиба С и D изгибающие моменты равны нулю, то эти точки можно рассматривать как шарниры).
, будет работать в тех же условиях, что и стержень при шарнирно-опертых концах (так как в точках перегиба С и D изгибающие моменты равны нулю, то эти точки можно рассматривать как шарниры).

Рис.3. Расчетная схема с жесткозакреплеными торцами.
Поэтому критическая сила для стержня с защемленными концами, длиной 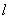 , равна критической силе для стержня основного случая длиной
, равна критической силе для стержня основного случая длиной 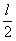 :
:
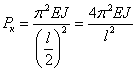
Полученные выражения можно объединить с формулой для критической силы основного случая и записать:
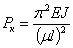
здесь 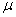 — так называемый коэффициент длины, равный:
— так называемый коэффициент длины, равный:
- при шарнирных концах (основной случай)
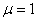 ,
, - одном свободном, другом защемленном
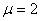 ,
, - обоих защемленных концах
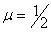 .
.
Для стержня, изображенного на рис.4, с одним защемленным, а другим шарнирно-опертым концами, коэффициент 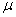 оказывается примерно равным
оказывается примерно равным 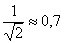 , а критическая сила:
, а критическая сила:
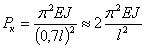
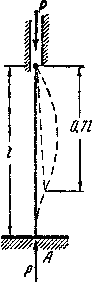
Рис.4. Потеря устойчивости стержня с одним жесткозакрепленным и другим шарнирно-опорным торцом
Величина 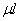 называется приведенной (свободной) длиной, при помощи коэффициента длины любой случай устройства опор стержня можно свести к основному; надо лишь при вычислении гибкости вместо действительной длины стержня ввести в расчет приведенную длину
называется приведенной (свободной) длиной, при помощи коэффициента длины любой случай устройства опор стержня можно свести к основному; надо лишь при вычислении гибкости вместо действительной длины стержня ввести в расчет приведенную длину 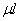 . Понятие о приведенной длине было впервые введено профессором Петербургского института инженеров путей сообщения Ф. Ясинским).
. Понятие о приведенной длине было впервые введено профессором Петербургского института инженеров путей сообщения Ф. Ясинским).
На практике, однако, почти никогда не встречаются в чистом виде те закрепления концов стержня, которые мы имеем на наших расчетных схемах.
Вместо шаровых опор обычно применяются цилиндрические шарниры. Подобные стержни следует считать шарнирно-опертыми при выпучивании их в плоскости, перпендикулярной к оси шарниров; при искривлении же в плоскости этих осей концы стержней следует считать защемленными (с учетом оговорок, приведенных ниже для защемленных концов).
В конструкциях очень часто встречаются сжатые стержни, концы которых приклепаны или приварены к другим элементам, часто еще с добавлением в месте прикрепления фасонных листов. Такое закрепление, однако, трудно считать защемлением, так как части конструкции, к которым прикреплены эти стержни, не являются абсолютно жесткими.
Между тем, достаточно возможности уже небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях, очень близких к шарнирному опиранию. Поэтому на практике недопустимо рассчитывать такие стержни, как стойки с абсолютно защемленными концами. Лишь в тех случаях, Когда имеет место очень надежное защемление концов, допускается небольшое (процентов на 10—20) уменьшение свободной длины стержня.
Наконец, на практике встречаются стержни, опирающиеся на соседние элементы по всей плоскости опорных поперечных сечений. Сюда относятся деревянные стойки, отдельно стоящие металлические колонны, притянутые болтами к фундаменту, и т. д. При тщательном конструировании опорного башмака и соединения его с фундаментом можно считать эти стержни имеющими защемленный конец. Сюда же относятся мощные колонны с цилиндрическим шарниром при расчете их на выпучивание в плоскости оси шарнира. Обычно же трудно рассчитывать на надежное и равномерное прилегание плоского концевого сечения сжатого стержня к опоре. Поэтому грузоподъемность таких стоек обычно мало превышает грузоподъемность стержней с шарнирно-опертыми концами.
Значения критических нагрузок могут быть получены в виде формул типа эйлеровой и для стержней переменного сечения, а также при действии нескольких сжимающих сил.
Лекция № 44. Пределы применимости формулы Эйлера
Казалось бы, что полученные в предыдущих параграфах результаты решают задачу проверки сжатого стержня на устойчивость; остается выбрать лишь коэффициент запаса 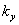 . Однако это далеко не так. Ближайшее же изучение числовых величин, получаемых по формуле Эйлера, показывает, что она дает правильные результаты лишь в известных пределах.
. Однако это далеко не так. Ближайшее же изучение числовых величин, получаемых по формуле Эйлера, показывает, что она дает правильные результаты лишь в известных пределах.
На рис.1 приведена зависимость величины критических напряжений, вычисленных при различных значениях гибкости для стали 3, обычно применяемой в металлических конструкциях. Эта зависимость представляется гиперболической кривой, так называемой «гиперболой Эйлеpa»: 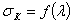
При пользовании этой кривой надо вспомнить, что представляемая ею формула 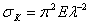 получена при помощи интегрирования дифференциального уравнения изогнутой оси, т. е. в предположении, что напряжения в стержне в момент потери устойчивости не превосходят предела пропорциональности.
получена при помощи интегрирования дифференциального уравнения изогнутой оси, т. е. в предположении, что напряжения в стержне в момент потери устойчивости не превосходят предела пропорциональности.
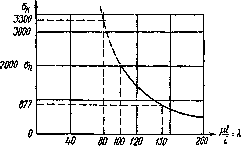
Рис.1. Гиперболическая зависимость критического напряжения от гибкости стержня
Следовательно, мы не имеем права пользоваться величинами критических напряжений, вычисленных по формуле Эйлера, если они получаются выше этого предела для данного материала. Иначе говоря, формула Эйлера применима лишь при соблюдении условия:
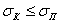 или
или 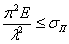
Если из этого неравенства выразить гибкость 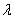 , то условие применимости формул Эйлера получит иной вид:
, то условие применимости формул Эйлера получит иной вид:
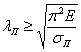
Подставляя соответствующие значения модуля упругости и предела пропорциональности для данного материала, находим наименьшее значение гибкости, при которой еще можно пользоваться формулой Эйлера. Для стали 3 предел пропорциональности может быть принят равным 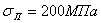 , поэтому, для стержней из этого материала можно пользоваться формулой Эйлера лишь при гибкости
, поэтому, для стержней из этого материала можно пользоваться формулой Эйлера лишь при гибкости
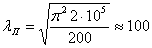
т. е. большей, чем 100 %
Для стали 5 при 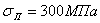 формула Эйлера применима при гибкости
формула Эйлера применима при гибкости 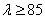 ; для чугуна — при
; для чугуна — при 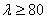 , для сосны — при
, для сосны — при 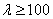 и т. д. Если мы на Рис.1 проведем горизонтальную линию с ординатой, равной
и т. д. Если мы на Рис.1 проведем горизонтальную линию с ординатой, равной 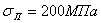 , то она рассечет гиперболу Эйлера на две части; пользоваться можно лишь нижней частью графика, относящейся к сравнительно тонким и длинным стержням, потеря устойчивости которых происходит при напряжениях, лежащих не выше предела пропорциональности.
, то она рассечет гиперболу Эйлера на две части; пользоваться можно лишь нижней частью графика, относящейся к сравнительно тонким и длинным стержням, потеря устойчивости которых происходит при напряжениях, лежащих не выше предела пропорциональности.
Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.
Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.
Необходимо сразу же отметить, что в настоящее время важнейшим источником для установления критических напряжений за пределом пропорциональности, т. е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.
Прежде всего надо выделить стержни с малой гибкостью, от 0 примерно до 30—40; у них длина сравнительно невелика по отношению к размерам поперечного сечения. Например, для стержня круглого сечения гибкости 20 соответствует отношение длины к диаметру, равное 5. Для таких стержней трудно говорить о явлении потери устойчивости прямолинейной формы всего стержня в целом в том смысле, как это имеет место для тонких и длинных стержней.
Эти короткие стержни будут выходить из строя главным образом за счет того, что напряжения сжатия в них будут достигать предела текучести 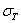 (при пластичном материале) или предела прочности
(при пластичном материале) или предела прочности 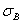 (при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 30
(при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 30  40, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или
40, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или 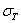 (сталь), или
(сталь), или 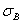 (чугун, дерево).
(чугун, дерево).
Таким образом, мы имеем два предельных случая работы сжатых стержней: короткие стержни, которые теряют грузоподъемность в основном за счет разрушения материала от сжатия, и длинные, для которых потеря грузоподъемности вызывается нарушением устойчивости прямолинейной формы стержня. Количественное изменение соотношения длины и поперечных размеров стержня меняет и весь характер явления разрушения. Общим остается лишь внезапность наступления критического состояния в смысле внезапного резкого возрастания деформаций.
В сжатых стержнях большой гибкости, для которых применима формула Эйлера, после достижения силой Р критического значения обычно наблюдается резкий рост деформаций. До этого момента прогибы, как правило, растут с ростом нагрузки, но остаются незначительными. Теоретически можно было бы ожидать, что до критической силы стержень будет оставаться прямым; однако ряд неизбежных на практике обстоятельств — начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, местные перенапряжения, неоднородность материала — вызывают небольшие прогибы и при сжимающих силах, меньших критических.
Подобный же характер имеет и зависимость укорочений от напряжения при сжатии коротких стержней; мы имеет ту же внезапность роста деформаций при определенной величине напряжений (когда 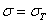 ).
).
Нам остается теперь рассмотреть поведение сжатых стержней при средних величинах гибкости, например для стальных стержней при гибкостях от 40 до 100; с подобными значениями гибкостей инженер чаще всего встречается на практике.
По характеру разрушения эти стержни приближаются к категории ^ тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.
Однако потеря прямолинейной формы и понижение критических напряжений по сравнению с короткими стержнями для этих стержней «средней» гибкости связаны с такими же явлениями нарушения прочности материала, какие вызывают потерю грузоподъемности в коротких стержнях. Здесь комбинируются и влияние длины, понижающее величину критических напряжений, и влияние значительного роста деформаций материала при напряжениях за пределом пропорциональности.
Экспериментальное определение критических сил для сжатых стержней производилось неоднократно как у нас, так и заграницей. Особенно обширный опытный материал собрал проф. Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.
На основании полученного опытного материала можно считать, что при критических напряжениях, меньших предела пропорциональности, все эксперименты подтверждают формулу Эйлера для любого материала.
Для стержней средней и малой гибкости были предложены различные эмпирические формулы, показывающие, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному:
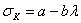
где а и b — коэффициенты, зависящие от материала, a 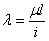 — гибкость стержня. Для литого железа Ясинский получил: а = 338,7МПа, b = 1,483 МПа. Для стали 3 при гибкостях от
— гибкость стержня. Для литого железа Ясинский получил: а = 338,7МПа, b = 1,483 МПа. Для стали 3 при гибкостях от 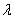 = 40 до
= 40 до 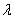 = 100 коэффициенты а и b могут быть приняты: а = 336 МПа; b = 1,47МПа. Для дерева (сосна): а = 29,3 МПа; b = 0,194 МПа.
= 100 коэффициенты а и b могут быть приняты: а = 336 МПа; b = 1,47МПа. Для дерева (сосна): а = 29,3 МПа; b = 0,194 МПа.
Иногда удобны эмпирические формулы, дающие для неупругой области изменение критических напряжений по закону квадратной параболы; к ним относится формула
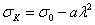
Здесь при 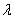 = 0 считают
= 0 считают 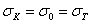 для пластичного и
для пластичного и 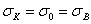 для хрупкого материала; коэффициент а, подобранный из условия плавного сопряжения с гиперболой Эйлера, имеет значение:
для хрупкого материала; коэффициент а, подобранный из условия плавного сопряжения с гиперболой Эйлера, имеет значение:
для стали с пределом текучести 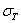 = 280 МПа а = 0,009 МПа
= 280 МПа а = 0,009 МПа
- сосны прочности
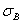 = 30; а = 0,0008 »
= 30; а = 0,0008 » - чугуна
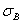 = 420; а = 0,044 »
= 420; а = 0,044 »
При наличии приведенных здесь данных может быть построен полный график критических напряжений (в зависимости от гибкости) для любого материала. На Рис.2 приведен такой график для строительной стали с пределом текучести 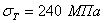 и пределом пропорциональности
и пределом пропорциональности 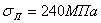 .
.
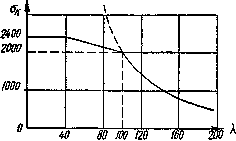
Рис.2. Полный график критических напряжений для строительной стали.
График состоит из трех частей: гиперболы Эйлера при 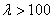 , наклонной прямой при
, наклонной прямой при 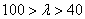 и горизонтальной, или слабо наклонной, прямой при
и горизонтальной, или слабо наклонной, прямой при 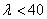 . Подобные же графики можно построить, комбинируя формулу Эйлера с результатами экспериментов, и для других материалов.
. Подобные же графики можно построить, комбинируя формулу Эйлера с результатами экспериментов, и для других материалов.
Таким образом, можно считать, что задача определения критических напряжений для стержней любой гибкости решена с достаточной для практических целей точностью.
Дата добавления: 2016-03-05; просмотров: 1057;
