Проверка сжатых стержней на устойчивость.
Ранее было отмечено, что для сжатых стержней должны быть произведены две проверки:
на прочность
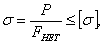
на устойчивость
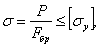 где
где 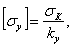
Для установления допускаемого напряжения на устойчивость нам остается теперь выбрать только коэффициент запаса k.
На практике этот коэффициент колеблется для стали в пределах от 1,8 до 3,0. Коэффициент запаса на устойчивость выбирается выше коэффициента запаса на прочность, равного для стали 1,5 — 1,6.
Это объясняется наличием ряда обстоятельств, неизбежных на практике (начальная кривизна, эксцентриситет действия, нагрузки, неоднородность материала и т. д.) и почти не отражающихся на работе конструкции при других видах деформации (кручение, изгиб, растяжение).
Для сжатых же стержней, ввиду возможности потери устойчивости, эти обстоятельства могут сильно снизить грузоподъемность стержня. Для чугуна коэффициент запаса колеблется от 5,0 до 5,5, для дерева — от 2,8 до 3,2.
Чтобы установить связь между допускаемым напряжением на устойчивость [ 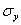 ] и допускаемым напряжением на прочность [
] и допускаемым напряжением на прочность [ 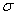 ], возьмем их отношение:
], возьмем их отношение:
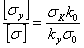 или<
или< 
Обозначая
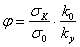
получим:
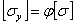
здесь 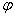 — коэффициент уменьшения основного допускаемого напряжения для сжатых стержней.
— коэффициент уменьшения основного допускаемого напряжения для сжатых стержней.
Имея график зависимости 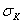 от
от 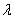 для данного материала, зная
для данного материала, зная 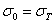 или
или 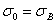 и выбрав коэффициенты запаса на прочность
и выбрав коэффициенты запаса на прочность 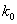 и на устойчивость
и на устойчивость 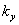 , можно составить таблицы значений коэффициента
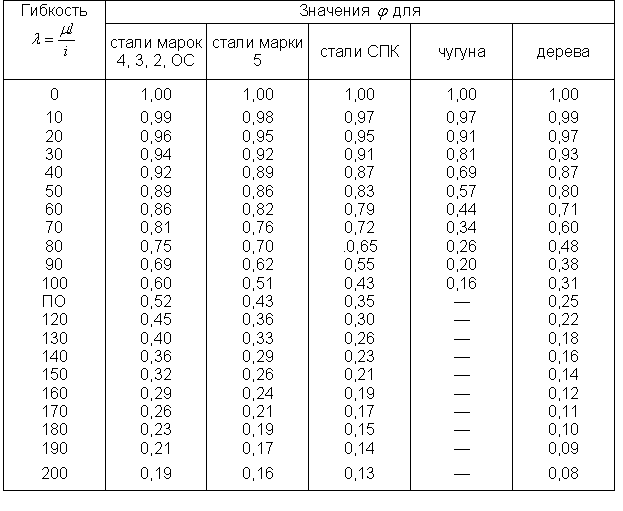
, можно составить таблицы значений коэффициента 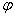 в функции от гибкости. Такие данные приводятся в наших технических условиях на проектирование сооружений; они сведены в таблицу.
в функции от гибкости. Такие данные приводятся в наших технических условиях на проектирование сооружений; они сведены в таблицу.
Пользуясь этой таблицей, можно произвести подбор сечения сжатого стержня. Так как величина площади сечения зависит от [ 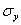 ], а это напряжение в свою очередь через коэффициент
], а это напряжение в свою очередь через коэффициент 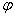 связано с гибкостью стержня
связано с гибкостью стержня 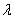 , т. е. с формой и размерами его сечения, то подбор приходится осуществлять путем последовательных приближений в таком, например, порядке.
, т. е. с формой и размерами его сечения, то подбор приходится осуществлять путем последовательных приближений в таком, например, порядке.
Выбираем форму сечения и задаемся его размерами; вычисляем наименьший радиус инерции и гибкость; находим по таблице коэффициент 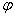 и вычисляем допускаемое напряжение на устойчивость
и вычисляем допускаемое напряжение на устойчивость 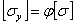 ; сравниваем действительное напряжение
; сравниваем действительное напряжение 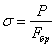 с величиной [
с величиной [ 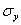 ]; если условие устойчивости
]; если условие устойчивости
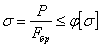
не удовлетворено, или удовлетворено с большим запасом, меняем размеры сечения и повторяем расчет. Конечно, окончательно выбранное сечение должно удовлетворять и условию прочности
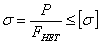
В практических расчетах условие устойчивости иногда записывается так:
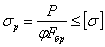
В левой части  представляет собой расчетное (условное) напряжение.
представляет собой расчетное (условное) напряжение.
Таблица.
Пример.
Подобрать двутавровое сечение стойки с одним защемленным концом, сжатой силами Р = 400 кН; длина стойки l=1,5 м. Основное допускаемое напряжение 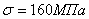 (Рис.3).
(Рис.3).

Рис.3. Расчетная схема сжатой стойки.
Так как в условии устойчивости 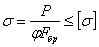 нам не известно ни
нам не известно ни 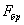 , ни
, ни 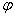 , одной из этих величин необходимо задаться. Примем для первого приближения
, одной из этих величин необходимо задаться. Примем для первого приближения 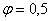 . В этом случае необходимая площадь поперечного сечения стержня будет равна
. В этом случае необходимая площадь поперечного сечения стержня будет равна
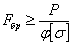 или
или 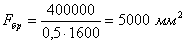
По сортаменту выбираем двутавр No 24, b с площадью  . Наименьший радиус инерции сечения
. Наименьший радиус инерции сечения 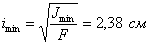 . Соответствующая гибкость стойки
. Соответствующая гибкость стойки 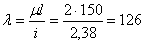
Коэффициент 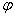 по интерполяции между значениями его из таблицы для
по интерполяции между значениями его из таблицы для  и
и 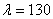 равен
равен 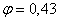 . Расчетным напряжением будет:
. Расчетным напряжением будет:
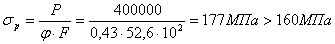
Перенапряжение составляет 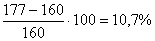 . Подбираем двутавр No 27, а.
. Подбираем двутавр No 27, а.  ;
; 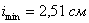 ; наибольшая его гибкость
; наибольшая его гибкость 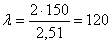 . Так как коэффициент
. Так как коэффициент 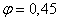 , то расчетное напряжение
, то расчетное напряжение
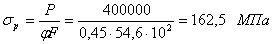
Перенапряжение составляет теперь 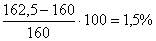 что допустимо.
что допустимо.
Лекция № 45. Прочность при циклически изменяющихся напряжениях.
Многие детали машин в процессе работы испытывают напряжения, циклически меняющиеся во времени. Так, например ось вагона, вращающаяся вместе с колесами (рис. 1), находятся под действием периодически меняющихся сил и испытывает циклически изменяющиеся напряжения, хотя внешние силы сохраняют свою величину.
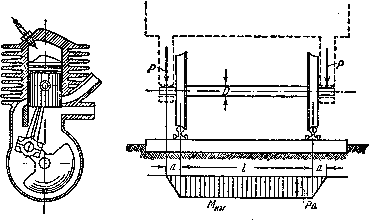
Рис.1. Расчетная схема оси вагона.
Для оси вагона на рис. 1 показана эпюра изгибающих моментов. В точке А поперечного сечения (рис. 2, а) имеем:
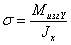
Расстояние y от точки А до нейтральной оси меняется во времени
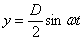
где 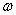 — угловая скорость вращения колеса.
— угловая скорость вращения колеса.
Следовательно,
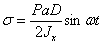
Таким образом, нормальное напряжение в сечениях оси меняется по синусоиде с амплитудой 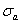 (рис. 2, б).
(рис. 2, б).
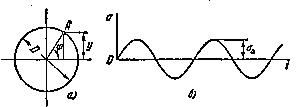
Рис.2. Изменение напряжения в точке А.
Опыт показывает, что при переменных напряжениях после некоторого числа циклов может наступить разрушение детали, в то время как при том же неизменном во времени напряжении 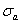 разрушения не происходит.
разрушения не происходит.

Рис.3. Иллюстрация усталостной прочности.
Число циклов до момента разрушения зависит от величины 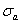 и меняется в весьма широких пределах. При больших напряжениях для разрушения бывает достаточно 5—10 циклов. Это хорошо видно хотя бы на примере многократного изгиба куска проволоки (рис. 3).
и меняется в весьма широких пределах. При больших напряжениях для разрушения бывает достаточно 5—10 циклов. Это хорошо видно хотя бы на примере многократного изгиба куска проволоки (рис. 3).
При меньших напряжениях деталь выдерживает миллионы и миллиарды циклов, а при еще меньших — способна работать неограниченно долго.
После разрушения на поверхности излома детали обнаруживаются обычно две ярко выраженные зоны ( рис. 4 и 5). В одной зоне кристаллы различаются невооруженным глазом с большим трудом. Поверхность излома имеет сглаженные очертания. В другой зоне явно выступают признаки свежего хрупкого разрушения. Кристаллы имеют острую огранку и блестящую чистую поверхность.
В целом создается первое впечатление, что подобного рода разрушение связано с изменением кристаллической структуры металла. Именно этим и объяснялось в свое время разрушение при циклических напряжениях. Описанное явление получило тогда название усталости, а направление исследований, связанных с прочностью, стало называться усталостной прочностью. В дальнейшем точка зрения на причины усталостного разрушения изменилась, но сам термин сохранился.
В настоящее время установлено, что структура металла при циклических нагрузках не меняется. Начало разрушения носит чисто местный характер. В зоне повышенных напряжений, обусловленных конструктивными, технологическими или структурными факторами, может образоваться микротрещина. При многократном изменении напряжений кристаллы, расположенные в зоне трещины, начинают разрушаться и трещина проникает в глубь тела.
Соприкасающиеся поверхности в зоне образовавшейся трещины испытывают контактное взаимодействие, в результате чего кристаллы истираются, а поверхности приобретают внешний вид мелкозернистой структуры. Так образуется одна из зон поверхности будущего излома.
В результате развития трещины сечение ослабляется. На последнем этапе происходит внезапное разрушение. Излом имеет характерную поверхность с неповрежденными чистыми кристаллами.
Из фотографии (рис. 4) видно, что разрушение бруса произошло в результате развития трещины, образовавшейся у края сечения. Разрушение рельса (рис. 5) обусловлено развитием трещины, образовавшейся внутри сечения в зоне местного порока.
Теоретический анализ усталостной прочности связан с большими трудностями. Природа усталостного разрушения обусловлена особенностями молекулярного и кристаллического строения вещества. Поэтому схема сплошной среды, которая с успехом применялась в рассматривавшихся до сих пор задачах, в данном случае не может быть принята в качестве основы для исследования.
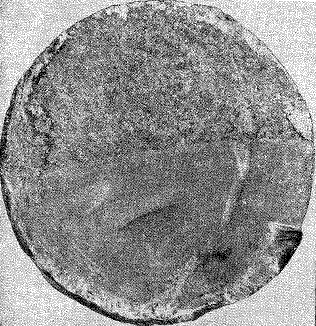
Рис.4. Характерные признаки уталостного разрушения

Рис.5. Характерные признаки усталостного разрушения рельсы
Для создания достаточно стройной теории усталостной прочности необходимо проникнуть в особенности строения кристаллов и межкристаллических связей с последующим привлечением аппарата статистики.
В настоящее время, однако, физические основы теории твердого тела не находятся еще на такой стадии развития, чтобы на их базе можно было бы создать методы расчета на усталостную прочность, удовлетворяющие запросам практики. Поэтому приходится идти по пути накопления экспериментальных фактов, из совокупности которых можно было бы выбрать подходящие правила как руководство для расчета. Объединение и систематика экспериментальных данных и представляет собой в настоящее время содержание теории усталостной прочности.
Отсутствие единых основополагающих законов в этой теории лишает ее стройности. В результате полученные экспериментальные зависимости не являются универсальными, а сами расчеты; дают сравнительно невысокую точность.
Дата добавления: 2016-03-05; просмотров: 2812;
