В СТЕРЖНЯХ ФЕРМЫ ДВУМЯ СПОСОБАМИ
Фермой называют шарнирно-стержневую геометрически неизменяемую конструкцию. По своим назначениям фермы бывают:
– мостовые (рис. 7.1.);
– кровельные, которые используются для поддержки покрытия зданий (рис. 7.2.);
– крановые (рис. 7.3.), которые используются в подъемных механизмах.
| 
| 
|
| Рисунок 7.1 | Рисунок 7.2 | Рисунок 7.3 |
Если все стержни фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, шарниры, называют узлами фермы.
Трением в шарнирах пренебрегают, стержни считаются невесомыми, а внешние силы прикладываются к узлам фермы. В этом случае стержни могут быть или растянутыми, или сжатыми.
Выделим фермы без лишних стержней – такие фермы, из которых нельзя снять ни одного стержня, не лишив их геометрически неизменной конструкции.
Зависимость между количеством стержней n и числом узлов k фермы без лишних стержней определяется формулой:
n = 2k - 3. (7.1)
Одновременно эта формула является условием статической определимости фермы, то есть такой, которую можно рассчитать методами статики твердого тела.
Рассчитать ферму в статике значит решить две задачи:
1. Определить реакции опор фермы;
2. Определить усилие во всех стержнях фермы.
| Усилие –это внутренняя сила, которая возникает в стержне под действием внешних сил. |
При решении первой задачи рассматривают ферму, как абсолютно твердое тело, воспользовавшись аксиомой затвердения (Дополнение Б). На схеме сил изображают заданные (активные) силы и реакции отброшенных связей.
Решение второй задачи базируется на положении: если вся ферма находится в равновесии, то и каждый ее элемент (узел, стержень, часть фермы) находится в равновесии. Это дает возможность определить усилия в стержнях фермы несколькими способами. Рассмотрим два основных способа определения усилий.
I способ - метод вырезания узлов;
II способ - метод сечения (метод Риттера).
Пример. Определить усилие в стержнях фермы, изображенной на рисунке 7.4, если к узлу Е приложена сила Р1 = 80 кН, а к узлу Д сила Р2 = 20 кН.
Рисунок 7.4
На данном этапе (не зная диаграмму Максвелла-Кремоны) невозможно определить усилия в стержнях фермы при неизвестных реакциях связей. Поэтому начнем с первой задачи.
1) Определение реакций опор в точках A и B.
Объект изучения – ферма, которую считаем абсолютно твёрдым телом, т.е. все шарниры затвердели (рис. 7.5). В точке В связь – невесомый стержень с шарнирными концами, потому реакция 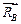 направлена вдоль стержня, например вверх (табл. 1.1, п. 3). Реакцию неподвижного шарнира раскладываем на две составляющие
направлена вдоль стержня, например вверх (табл. 1.1, п. 3). Реакцию неподвижного шарнира раскладываем на две составляющие 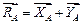 (табл. 1.1, п. 4). На рисунке 7.5 изображаем схему сил, которые действуют на всю свободную от связей ферму. Дальше действуем по алгоритму (тема 2, п. 2.4). Вид системы сил, изображенной на рисунке 7.5 – произвольная плоская.
(табл. 1.1, п. 4). На рисунке 7.5 изображаем схему сил, которые действуют на всю свободную от связей ферму. Дальше действуем по алгоритму (тема 2, п. 2.4). Вид системы сил, изображенной на рисунке 7.5 – произвольная плоская.

Рисунок 7.5
Уравнений равновесия составляем три (формула (5.6)), неизвестных – три. Задача статически определена. Уравнения равновесия:
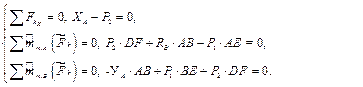
Учитывая, что длины горизонтальных и вертикальных стержней одинаковы, обозначим их длину а. Имеем
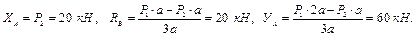
Сделаем проверку
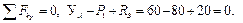
2) Определение усилий в стержнях методом вырезания узлов
Последовательно вырезается каждый узел фермы и рассматривается его равновесие под действием приложенных к нему сил. Реакции связей в точках A и B теперь считаются известными силами. На каждый узел действуют реакции разрезанных стержней, которые этот узел образовали. Система сил, которые действуют на вырезанный узел, обычно, будет плоской системой сходящихся сил. Равновесие сходящейся плоской системы сил, как известно, обеспечивается выполнением уравнений (формулы (2.6)) 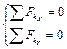 , или построением замкнутого
, или построением замкнутого
силового многоугольника. Из-за того, что уравнений равновесия – два, надо начинать с узла, в котором сходятся только двастержня. В нашем примере можно начинать или с узла А, или с узла В.
Дата добавления: 2016-03-15; просмотров: 1688;
