Тема 9. РЫЧАГ. СТОЙКОСТЬ ПРИ ПЕРЕКИДЫВАНИИ
| Рычагом называют твердое тело, которое имеет неподвижную ось вращения, а силы, действующие на него , лежат в плоскости, перпендикулярной к этой оси (рис. 9.1, 9.5). |
 Силы
Силы 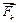 (k = 1, 2,…, n )принадлежат плоскости Оxy, ось
(k = 1, 2,…, n )принадлежат плоскости Оxy, ось 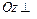 пл. Оxy (рис.9.1). Если нас интересует вопрос: чему равна реакция неподвижного шарнира в т. О, то надо действовать по алгоритму (п. 2.4). Конечно, будем составлять три уравнения равновесия (формулы (5.5), например). Но на практике иногда возникают задачи, связанные с вопросом, : какими должны быть активные силы
пл. Оxy (рис.9.1). Если нас интересует вопрос: чему равна реакция неподвижного шарнира в т. О, то надо действовать по алгоритму (п. 2.4). Конечно, будем составлять три уравнения равновесия (формулы (5.5), например). Но на практике иногда возникают задачи, связанные с вопросом, : какими должны быть активные силы  , которые обеспечат равновесие рычага, то есть условие, при котором тело не будет вращаться вокруг оси Оz. При этом реакция связи в точке О нас не интересует.
, которые обеспечат равновесие рычага, то есть условие, при котором тело не будет вращаться вокруг оси Оz. При этом реакция связи в точке О нас не интересует.
Примерами таких задач являются:
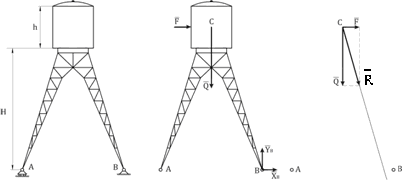
– выяснить условие, при котором водонапорная башня не будет опрокидываться под давлением ветра (рис. 9.2 а);
– найти наименьшую ширину плотины а при разных силах давления воды слева и справа (рис. 9.3);
– найти величину G1 противовеса, при котором подъемный кран (рис. 9.4) не опрокинется.
| ||
| а | б | в |
Рисунок 9.2

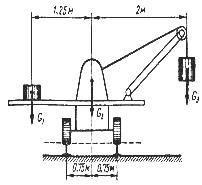
Рисунок 9.3 Рисунок 9.4
В таком случае вместо трех уравнений равновесия [1] 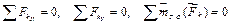 составляется одно – уравнение моментов, в которое не входят неизвестные реакции связи
составляется одно – уравнение моментов, в которое не входят неизвестные реакции связи  (рис. 9.1). Третье уравнение и является условием которому должны удовлетворять активные силы, действующие на рычаг, если он находится в равновесии. Это условие формулируется так:
(рис. 9.1). Третье уравнение и является условием которому должны удовлетворять активные силы, действующие на рычаг, если он находится в равновесии. Это условие формулируется так:
| Если рычаг находится в равновесии, то алгебраическая сумма моментов всех заданных сил, действующих на рычаг, относительно опорной точки равна нулю |
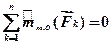 . (9.1)
. (9.1)
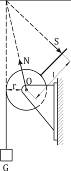 Рисунок 9.5
Рисунок 9.5
| Определим, например, усилие S (рис. 9.5), которое надо приложить к рукоятке ворота, чтобы удержать груз G. Радиус барабана r, расстояние от оси барабана к точке приложения усилия руки l.
Из уравнения равновесия (9.1) имеем  , , 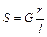 , если r = 0,2 м, l = 0,8 м, G = 1000 Н, S = 250 Н.
Уравнение (9.1) есть, вместе с тем, и условием устойчивости тел при опрокидывании. Рассмотрим это условие для водонапорной башни (рис. 9.2). Схема сил, которые действуют на башню, если ветер давит слева, показана на рис. 9.2 б, где , если r = 0,2 м, l = 0,8 м, G = 1000 Н, S = 250 Н.
Уравнение (9.1) есть, вместе с тем, и условием устойчивости тел при опрокидывании. Рассмотрим это условие для водонапорной башни (рис. 9.2). Схема сил, которые действуют на башню, если ветер давит слева, показана на рис. 9.2 б, где 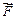 – сила давления ветра, – сила давления ветра,  – вес цистерны. – вес цистерны.
|
Считаем, что имеем критическую ситуацию, когда башня уже не имеет контакта с землей в точке А, но может вращаться вокруг оси, проходящей через шарнир В.
Уравнение (9.1) в этом случае имеет вид:
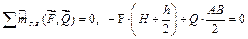
Отсюда можно выяснить, например, каким должно быть расстояние между опорами А и В, чтобы башня не опрокинулась вправо.
Назовем абсолютные величины моментов сил 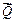 и
и 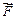 относительно точки В, удерживающим и опрокидывающим моментами, соответственно
относительно точки В, удерживающим и опрокидывающим моментами, соответственно
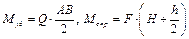 .
.
На границе устойчивости (критическая ситуация) удерживающий момент равен опрокидывающему моменту
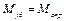 .
.
| Для устойчивого состояния равновесия тела нужно, чтобы удерживающий момент был больше, чем момент опрокидывающий, то есть |
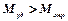 (9.2)
(9.2)
Устойчивость при опрокидывании в технике принято определять так называемым коэффициентом устойчивости. Коэффициент устойчивости равен отношению удерживающего момента к опрокидывающему моменту
 . (9.3)
. (9.3)
В случае критического состояния k = 1, в случае устойчивого состояния равновесия k > 1.
Исследовать опрокинется ли башня под действием силы 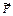 или нет, можно и графическим способом (рис. 9.2 в). Для этого нужно:
или нет, можно и графическим способом (рис. 9.2 в). Для этого нужно:
– найти равнодействующую  сил
сил 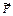 и
и 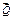 (продолжив линии действия этих сил, и отложив силы в масштабе)
(продолжив линии действия этих сил, и отложив силы в масштабе) 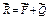 ;
;
– выяснить знак момента силы  относительно точки В. Если знак момента силы
относительно точки В. Если знак момента силы  относительно точки В плюс, (то есть линия действия силы
относительно точки В плюс, (то есть линия действия силы  находится слева от точки В) – состояние равновесия устойчивое. Если знак момента – минус, (то есть сила
находится слева от точки В) – состояние равновесия устойчивое. Если знак момента – минус, (то есть сила  находится справа от точки В) – состояние равновесия неустойчивое. Если
находится справа от точки В) – состояние равновесия неустойчивое. Если 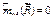 (то есть сила
(то есть сила  проходит через точку В) – имеем состояние критического равновесия.
проходит через точку В) – имеем состояние критического равновесия.
Вопросы для самоконтроля по теме 9
1. Что называют рычагом? Сформулируйте условие равновесия рычага.
2. Чему равен коэффициент устойчивости при опрокидывании? Что нужно для устойчивого состояния равновесия?
Дата добавления: 2016-03-15; просмотров: 1191;
