Определение координат центра тяжести тела
На все части тела, расположенные в области притяжения Земли, действуют силы притяжения к Земле. Эти силы называют силами притяжения, или силами тяжести. Размеры реальных тел намного меньше радиуса Земли. Поэтому можно считать, что силы земного притяжения, которые действуют на элементарные части тела, с достаточно большой точностью образуют систему параллельных сил.
| Равнодействующая сил тяжестей отдельных частей тела называется силой тяжести тела. |
Следовательно, сила тяжести тела равна 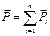 и приложена в центре параллельных сил тяжестей частей тела – центре тяжести тела. На рисунке 10.3 центр тяжести обозначен буквой С.
и приложена в центре параллельных сил тяжестей частей тела – центре тяжести тела. На рисунке 10.3 центр тяжести обозначен буквой С.
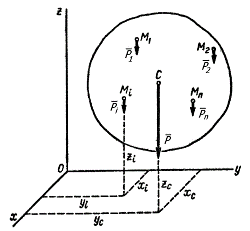
Рисунок 10.3
Координаты точки С можно найти по формулам (10.8), где Pi – вес отдельной части тела, а xi,, yi, zi – координаты этой точки приложения силы 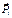 .
.
Для тел, вес которых распределен непрерывно по его объему, знак суммы можно заменить интегралом и формулы (10.8) приобретают вид
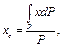
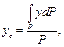
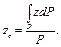 (10.9)
(10.9)
Рассмотрим некоторые частные случаи.
1. Однородное объемное тело. Если удельный вес тела постоянная величина, j = const, тогда
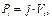
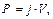 (10.10)
(10.10)
где Vi – объем части тела;
V – объем всего тела.
Подставим формулу (10.10) в формулу (10.8). После сокращения на j, имеем
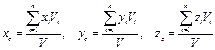 (10.11)
(10.11)
или, с учетом формулы (10.9),
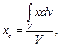
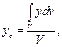
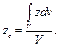 (10.12)
(10.12)
2. Однородное плоское тело. Пусть однородное плоское тело расположено в плоскости Оxy (рис. 10.4): j – вес единицы площади тела; Si – площадь элементарной его части; S – площадь всего тела.
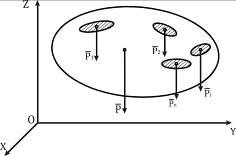 Рисунок 10.4
Рисунок 10.4
| Тогда 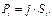 , , 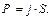 (10.13)
Подставив (10.13) в формулы (10.8) и (10.9), имеем формулы для определения координат центра тяжести однородного плоского тела (пластины) (10.13)
Подставив (10.13) в формулы (10.8) и (10.9), имеем формулы для определения координат центра тяжести однородного плоского тела (пластины)
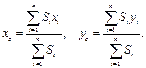 (10.14) (10.14)
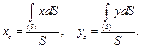 (10.15) (10.15)
|
3. Однородное линейное тело (провод, стержневая конструкция, рис. 10.5).
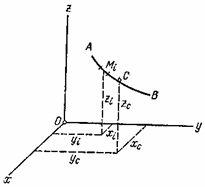 Рисунок 10.5
Рисунок 10.5
| Обозначим j – вес единицы длины однородного линейного тела. Тогда его вес и вес его элементарной части определяются формулами
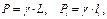 (10.16)
где L – длина тела;
li –- длина i-го элемента.
Подставив формулу (10.16) в формулы (10.8) и (10.9), имеем (10.16)
где L – длина тела;
li –- длина i-го элемента.
Подставив формулу (10.16) в формулы (10.8) и (10.9), имеем
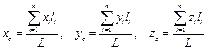 (10.17) (10.17)
|
или 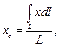
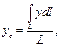
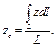 (10.18)
(10.18)
Дата добавления: 2016-03-15; просмотров: 1187;
