Метод разбиения тела на тела, положение центров тяжести которых известно
Для определения положения центра тяжести тела сложной геометрической формы, их мнимо разбивают на части, положение центров тяжестей которых известно. Этот способ применяется и тогда, когда у тела есть вырезы (пустоты). В формулах (10.11) и (10.14), которые в данном методе применяются, количество слагаемых равняется количеству тел, на которые разбили тело сложной формы.
Объемы, или площади тех тел, из которых образованы вырезы или пустоты, в формулах (10.11) или (10.14) берем с отрицательным знаком.
Покажем применение этого метода на примерах.
Пример 1.
Найти центр тяжести заштрихованной площади детали.
 Эту площадь можно рассматривать как фигуру, которая состоит из прямоугольника, из которого вырезали полукруг и сверху добавили треугольник. Обозначим фигуры номерами: прямоугольник – 1, полукруг – 2, треугольник - 3.
Эту площадь можно рассматривать как фигуру, которая состоит из прямоугольника, из которого вырезали полукруг и сверху добавили треугольник. Обозначим фигуры номерами: прямоугольник – 1, полукруг – 2, треугольник - 3.
Координаты точки С определяем по формулам (10.14) :
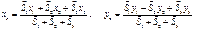 ,
,
где  – площади элементов (фигур) 1, 2, 3, взятые с определенными знаками;
– площади элементов (фигур) 1, 2, 3, взятые с определенными знаками;
(х1у1), (х2у2), (х3у3) – координаты точек С1, С2, С3 – центров тяжестей соответствующих фигур.
Занесём необходимые для подсчетов данные в таблицу, помня, что площадь 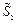 вырезали потому, что она имеет знак
вырезали потому, что она имеет знак
« – » (метод отрицательных площадей).
Таблица 10.1
| Номер элемента | Площадь  ,
см2 ,
см2
| хi, см | yi, см | 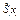 , см3 , см3
| 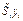 , см3 , см3
|
| 32×4 | 32×2 | ||||
| – 4,5 π | 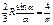
| – 4 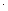 4,5 π 4,5 π
| 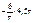
| ||
| 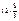
| 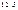
| |||
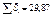
| 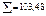
| 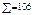
|
Ответ хС ≈ 3,46 см, уС ≈ 3,54 см.
Пример 2.
Твердое тело состоит:
– из однородного цилиндра 1, радиусы которого: внешний R и внутренний r, а высота Н;
однородного сплошного конуса 2, радиус основания которого равен R, а высота h. Определить положение центра тяжести твердого тела (рис. 10.10).
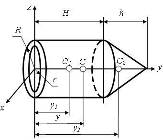 Рисунок 10.10
Рисунок 10.10
|
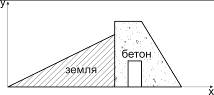 Рисунок 10.11
Рисунок 10.11
|
Начало координат выберем в центре основания цилиндра, ось y – ось симметрии тела. Поэтому координаты xc = zc = 0. Ищем координату yc по формуле (10.11).
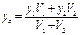 ,
,
где у1, у2 – координаты центров тяжестей цилиндра и конуса, соответственно,
V1, V2 – объемы цилиндра и конуса, соответственно.
Учитывая, что 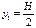 ,
, 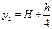 (потому что центр тяжести конуса, как и пирамиды, находятся на расстоянии
(потому что центр тяжести конуса, как и пирамиды, находятся на расстоянии  от плоскости основания)
от плоскости основания) 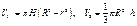 , имеем
, имеем
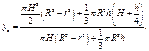
Этот метод можно применить не только для однородных тел. Для неоднородных тел нужно пользоваться формулами (10.8), потому что удельный вес у каждого тела, из которого состоит составленное тело, свой. Например, в плотине (рис. 10.11), которая построена из бетона и земляной почвы, γ бетона и γ земляной почвы –разные.
Дата добавления: 2016-03-15; просмотров: 1191;
