Методы определения координат центра тяжести тела

Метод симметрии

Пользуясь свойствами интегралов, можно легко установить следующие положения: если однородное твердое тело имеет элемент симметрии (плоскость, или ось, или центр), то центр тяжести этого тела находится на этом элементе (в этой плоскости, или на этой оси, или в этом центре) симметрии.

Воспользовавшись этим методом, получим центры тяжести площади параллелограмма и треугольника. Из курса математики средней школы известно, что точка пересечения диагоналей параллелограмма является центром его симметрии. Следовательно, центр тяжести параллелограмма (прямоугольника, ромба) находится в точке пересечения его диагоналей.

 

Для нахождения центра тяжести площади треугольника ABD (рис. 10.6) разобьем его площадь на огромное количество полосок малой ширины параллельно к стороне AD.

 

Рисунок 10.6

Центр тяжести каждой полоски находится в ее центре, то есть на медиане ВК. Разбивая треугольник на полоски линиями, параллельными к стороне АВ, получим, что центр тяжести каждой полоски лежит на медиане DM.

 

Вывод.

Центр тяжести площади треугольника находится в точке пересечения его медиан. В аналитической геометрии доказывается, что координаты точки пересечения медиан треугольника определяются формулами

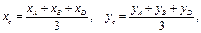
где 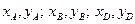– координаты вершин треугольника A, B и D, соответственно.