Центр системы параллельных сил

Вспомним, как сложить две параллельные силы , которые сонаправлены (рис. 10.1).

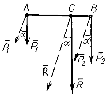Рисунок 10.1	Как известно, равнодействующая этих сил равна по модулю сумме сил и приложенных в точке С, которая разделяет расстояние АВ на отрезки, обратно пропорциональные силам. То есть . Вопрос: когда мы повернем силы на один и тот же угол α, что будет с равнодействующей? Ответ: равнодействующая также повернется на угол α и останется приложенной в той же точке. Это напоминает центр тяжести тела : как бы мы не поворачивали тело – его центр тяжести остается в той же точке.
	Центром системы параллельных сил называют точку С – точку приложения равнодействующей этой системы сил. При повороте параллельных сил на один и тот же угол положение точки С не меняется.

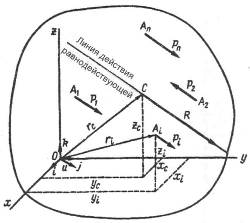
Определим положение центра параллельных сил, если известны координаты точек приложения сил (рис.10.2).

Рисунок 10.2

Будем считать, что точки фиксированы, то есть сила не является скользящим вектором. Кроме того, из-за того, что все силы параллельны какому-то одному единичному вектору (некоторые силы с ним совпадают, некоторые противоположно направлены), зададим силы формулой

, (10.3)

где – алгебраическое значение силы, то есть учитываем знак «+» или «–» в зависимости от направления силы .

Для равнодействующей системы параллельных сил имеем

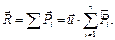(10.4)

Из-за того, что система параллельных сил приводится к равнодействующей, имеет место теорема Вариньона относительно точки О. По формуле (10.1)

.

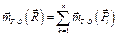Для векторных моментов относительно точки О , согласно формуле (6.2) имеем 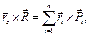(10.5)

где 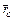– радиус-вектор центра параллельных сил точки С, проведенный из т. О;

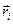– радиус–вектор точки 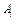, в которой приложена сила , проведенный из т. О.

Если подставить формулы (10.3) и (10.4) в (10.5), то после перенесения всех слагаемых в левую часть равенства и вынесения за скобки общего множителя 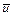, получим

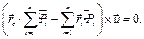(10.6)

Из-за того что это равенство имеет место при произвольном по направлению векторе 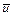, то это возможно только тогда, когда скобка равна нулю, то есть

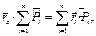или

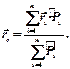(10.7)

По формуле (10.7) определяют радиус - вектор центра параллельных сил, если заданы силы и точки их приложения.

В проекциях на оси координат из формулы (10.7) получим формулы для определения координат центра параллельных сил :

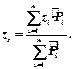(10.8)

Суммы, которые содержатся в числителях формул (10.8), называются статичными моментами системы параллельных сил относительно координатных плоскостей.

Для плоской системы параллельных сил, которые расположены в плоскости Оxy, вместо формул (10.8), будут только первые две формулы. Суммы 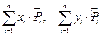в этом случае называют статичными моментами относительно координатных осей.