Реакция шероховатой поверхности. Угол и конус трения
Реакция идеально гладкой поверхности, как известно, независимо от приложенных к телу сил, направлена по нормали к касательной плоскости (рис. 1.11 б). Реакция же реальной (шероховатой) поверхности состоит из двух сил: нормальной реакции  и силы сцепления
и силы сцепления 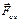 или силы трения (рис. 8.3).
или силы трения (рис. 8.3).
 Рисунок 8.3
Рисунок 8.3
|
Сила сцепления при этом, как мы убедились из опыта (рис. 8.1), – величина переменная. Поэтому, полная реакция шероховатой поверхности образует угол 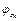 с нормалью к поверхности. Тангенс угла сцепления равен коэффициенту сцепления с нормалью к поверхности. Тангенс угла сцепления равен коэффициенту сцепления
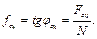 (8.3) (8.3)
|
| Угол, тангенс которого равен коэффициенту трения скольжения, называют углом трения скольжения φ. |
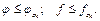
Угол сцепления можно определить экспериментальным путем. Прибор для определения угла трения, а значит и коэффициента трения, очень простой. Он состоит из наклонной плоскости ОА (рис. 8.4), на которую помещают тело из того материала, коэффициент трения которого с материалом наклонной плоскости хотят определить.
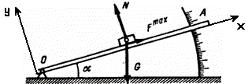 Рисунок 8.4
Рисунок 8.4
| Угол наклона α плоскости к горизонту можно менять. Зафиксируем угол α, при котором тело находится в предельном состоянии покоя (следовательно, сила сцепления достигла максимального значения). Определим значение угла α. |
Для этого составим уравнения равновесия сходящейся плоской системы сил, которая прикладывается к телу (формула (2.6)). Ось Ох направим по стержню ОА, ось Оy перпендикулярна к стержню
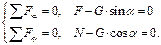
Имеем 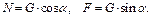 Вместе с этим,
Вместе с этим, 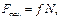 поэтому
поэтому
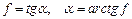 . (8.4)
. (8.4)
Величину коэффициента f для соответствующих материалов (тело – плоскость) можно определить по таблице тангенсов.
| Конус с вершиной в точке контакта тел, образующая которого создает угол φ с нормалью к контактирующим поверхностям, называют конусом трения. Образующая этого конуса совпадает с максимальной реакцией опорной поверхности. |
Полная реакция поверхности на тело 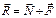 будет менять свое направление, если будут попытки сдвинуть тело 1 (рис. 8.3) в разных направлениях по поверхности. Если коэффициент трения во всех направлениях одинаков, то конус трения – круговой. Если коэффициент трения в разных направлениях неодинаков (напр., для деревянной поверхности) – конус трения будет некруговым. Некоторые задачи на равновесие с учетом сил трения рационально решать с помощью конуса трения или угла трения.
будет менять свое направление, если будут попытки сдвинуть тело 1 (рис. 8.3) в разных направлениях по поверхности. Если коэффициент трения во всех направлениях одинаков, то конус трения – круговой. Если коэффициент трения в разных направлениях неодинаков (напр., для деревянной поверхности) – конус трения будет некруговым. Некоторые задачи на равновесие с учетом сил трения рационально решать с помощью конуса трения или угла трения.
Пусть активные силы, которые действуют на тело, приводятся к одной силе 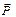 , которая образует угол
, которая образует угол 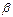 с нормалью (рис. 8.5).
с нормалью (рис. 8.5).

|
Реакция шероховатой поверхности на тело состоит из двух составляющих 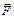 и и 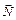 .
Уравнения предельного равновесия, когда сила .
Уравнения предельного равновесия, когда сила 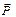 не сдвинет тело с места, имеют вид не сдвинет тело с места, имеют вид
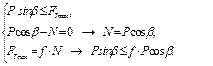
|
Рисунок 8.5
Независимо от величины активной силы 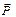 , имеет место зависимость между углами в случае предельного равновесия
, имеет место зависимость между углами в случае предельного равновесия 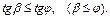 Если активная сила
Если активная сила  приложена вне угла трения (рис. 8.6), то есть
приложена вне угла трения (рис. 8.6), то есть 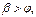 тогда
тогда 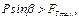
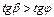 – тело сдвинется с места.
– тело сдвинется с места.
Вывод.
| Никакая (достаточно большая) сила не «выведет» тело из равновесия, если ее линия действия (рис. 8.5) проходит внутри конуса трения. | ||
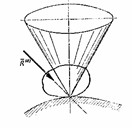 Рисунок 8.6
Рисунок 8.6
|
|
Пример. Рассмотрим равновесие тяжелого бруса АВ, который опирается на две шероховатые плоскости в точках А и В (рис. 8.7). Коэффициенты трения 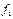 и
и  известны, поэтому можно показать углы трения
известны, поэтому можно показать углы трения  и
и  , отложив их от нормалей к плоскостям, на которые опирается брус.
, отложив их от нормалей к плоскостям, на которые опирается брус.
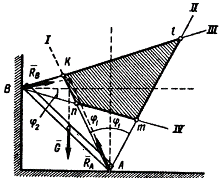 Рисунок 8.7
Рисунок 8.7
|
Если из точки А провести линии 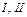 , а из точки В провести линии , а из точки В провести линии 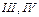 , получим границы конусов трения для горизонтальной и вертикальной опорных плоскостей. Четырехугольник, образованный этими линиями, внутри которого будут пересекаться линии действия реакций опор в точках А и В, называют областью равновесия для данной задачи. , получим границы конусов трения для горизонтальной и вертикальной опорных плоскостей. Четырехугольник, образованный этими линиями, внутри которого будут пересекаться линии действия реакций опор в точках А и В, называют областью равновесия для данной задачи.
|
Брус находится в равновесии под действием трех сил : силы тяжести 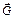 , реакций опор в точках А и В. Силы должны лежать в области равновесия, потому что при равновесии тела под действием трех сил - силы пересекаются в одной точке (п. 2.3). Поэтому равновесие будет только в том случае, когда линия действия силы тяжести
, реакций опор в точках А и В. Силы должны лежать в области равновесия, потому что при равновесии тела под действием трех сил - силы пересекаются в одной точке (п. 2.3). Поэтому равновесие будет только в том случае, когда линия действия силы тяжести 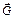 пересекает область равновесия. Если линия действия силы
пересекает область равновесия. Если линия действия силы 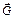 пройдет через точку К – это предельное состояние покоя.
пройдет через точку К – это предельное состояние покоя.
Трение качения
Если тело имеет форму цилиндрического катка и под действием активных сил может катиться по поверхности другого тела, то из-за деформации опорной поверхности этих тел в месте контакта возникают силы реакции, которые мешают как скольжению, так и качению.
 Пусть к оси катка весом
Пусть к оси катка весом 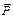 приложена горизонтальная сила
приложена горизонтальная сила 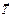 (рис. 8.8). Контакт катка с плоскостью из-за деформации происходит не в одной точке, как в случае абсолютно твердых тел, а по некоторой площадке DЕ. Точка приложения сил
(рис. 8.8). Контакт катка с плоскостью из-за деформации происходит не в одной точке, как в случае абсолютно твердых тел, а по некоторой площадке DЕ. Точка приложения сил  и
и 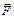 будет находиться в некоторой точке Е этой площадки. Эта точка будет сдвинута по сравнению с точкой D в направлении возможного движения тела.
будет находиться в некоторой точке Е этой площадки. Эта точка будет сдвинута по сравнению с точкой D в направлении возможного движения тела.
Изображенную на рис. 8.8 схему сил можно рассматривать, как систему двух пар сил ( 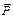 ,
,  ) и (
) и ( 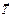 ,
, 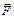 ). Имеем уравновешенную систему пар
). Имеем уравновешенную систему пар 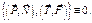
Пара сил ( 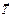 ,
, 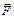 ) стремится привести каток в движение; пара сил (
) стремится привести каток в движение; пара сил ( 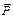 ,
,  ) создает сопротивление качению.
) создает сопротивление качению.
Момент пары сил ( 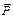 ,
,  ) называется моментом сопротивления качению. Таким образом, реакция плоскости на каток состоит из нормальной реакции
) называется моментом сопротивления качению. Таким образом, реакция плоскости на каток состоит из нормальной реакции  , касательной реакции
, касательной реакции 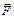 и из пары трения качения (
и из пары трения качения ( 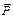 ,
,  ).
).
Пренебрегая глубиной впадины, на которую деформировал каток поверхность, имеем: у пары сил ( 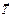 ,
, 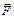 ) плечо равно радиусу катка, а у пары сил (
) плечо равно радиусу катка, а у пары сил ( 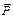 ,
,  ) плечо
) плечо 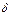 . При критическом равновесии моменты этих пар по модулю равны между собой и равны моменту сопротивления качению, то есть
. При критическом равновесии моменты этих пар по модулю равны между собой и равны моменту сопротивления качению, то есть
 . (8.5)
. (8.5)
Установлены приближенные законы трения качения.
Первый закон.
| Максимальный момент пары сил сопротивления качению не зависит от радиуса катка и, пропорционален силе нормального давления катка |
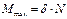 . (8.6)
. (8.6)
Второй закон.
Коэффициент трения качения 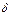 равен плечу пары сил сопротивления качению при предельном равновесии катка. равен плечу пары сил сопротивления качению при предельном равновесии катка.
|
Коэффициент трения качения зависит от материалов контактирующих поверхностей, а также от физического состояния этих поверхностей. Коэффициенты трения устанавливают экспериментально. Некоторые значения коэффициентов трения качения: дерево по стали 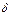 = 0,0004 м; колесо вагона по рельсу
= 0,0004 м; колесо вагона по рельсу 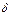 = 5·10-5 м; резиновая шина по шоссе
= 5·10-5 м; резиновая шина по шоссе 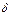 = 0,0024 м.
= 0,0024 м.
На основе рис. 8.9 легко установить условие чистого качения (скольжение отсутствует).
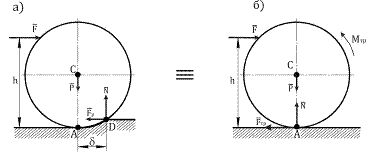
Рисунок 8.9
Скольжение будет отсутствовать, если 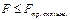 из-за того, что
из-за того, что  , то есть
, то есть 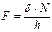 , а
, а 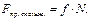
Имеем  отсюда получим
отсюда получим
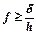 , (8.7)
, (8.7)
что является условием чистого качения цилиндрического тела по поверхности. В этой формуле:
f – коэффициент трения скольжения;
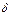 – коэффициент трения качения;
– коэффициент трения качения;
h – расстояние точки приложения активной силы от опорной поверхности.
Как видим, для большинства материалов отношение 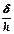 значительно менше коэффициента трения скольжения
значительно менше коэффициента трения скольжения 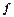 . Именно потому в технике, когда это возможно, трение скольжения стремятся заменить трением качения (колёса, катки, шариковые подшипники и т.д.)
. Именно потому в технике, когда это возможно, трение скольжения стремятся заменить трением качения (колёса, катки, шариковые подшипники и т.д.)
Вопросы для самоконтроля по теме 8
1. Если сила сцепления не достигла максимального значения, будет ли иметь задача о равновесии тела единственное решение? Почему?
2. Существует ли сила, линия действия которой лежит внутри конуса трения, которая выведет это тело из состояния покоя? Докажите это.
3. Как в технике используют тот факт, что коэффициенты трения скольжения и трения качения разные?
4. Что называют конусом трения? Что называют углом трения?
Дата добавления: 2016-03-15; просмотров: 4179;
