Всякое уравнение второй степени с тремя неизвестными определяет эллипсоид, гиперболоид, параболоид, конус, цилиндр или две плоскости
Поверхность второго порядка в пространстве задаётся следующим общим уравнением:
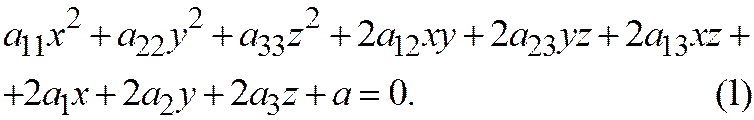
Общее уравнение поверхности второго порядка (1), заданное относительно ДПСК (как было установлено ранее) выражает одну из 17 поверхностей.
Теорема 1. В таблице 1 даны необходимые и достаточные признаки каждого из 17 классов поверхностей второго порядка.
Таблица 1
| № | Название Поверхности | Признак поверхности |
| Эллипсоид | 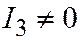 , , 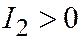 , , 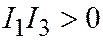 , , 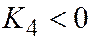 . .
| |
| Мн. эллипсоид | 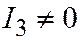 , , 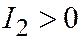 , , 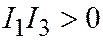 , , 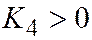 . .
| |
| Мнимый конус | 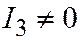 , , 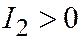 , , 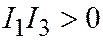 , , 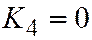 . .
| |
| Однопол. гиперб. | 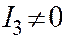 , , 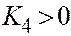 , и, или , и, или  , или , или 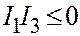 . .
| |
| Двупол. гиперб. | 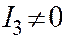 , ,  , и, или , и, или  , или , или 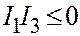 . .
| |
| Конус 2-го поряд | 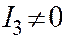 , , 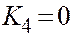 , и, или , и, или  , или , или 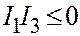 . .
| |
| Эллипт. парабол. | 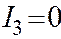 , ,  . .
| |
| Гиперб. парабол. | 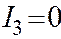 , , 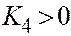 . .
| |
| Эллипт. цилиндр | 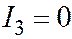 , , 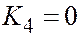 , , 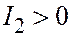 , , 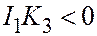 . .
| |
| Мн. Элл. цилинд. | 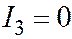 , , 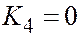 , , 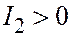 , , 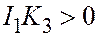 . .
| |
| 2 мн. пер. плоск. | 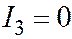 , , 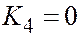 , , 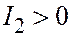 , , 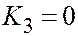 . .
| |
| Гиперб. цилиндр | 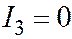 , , 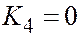 , , 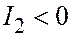 , , 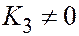 . .
| |
| 2 пересек. плоск. | 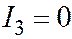 , , 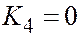 , , 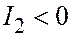 , , 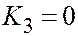 . .
| |
| Парабол. цилинд. | 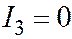 , , 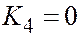 , , 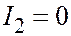 , , 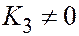 . .
| |
| 2 паралл. плоск. | 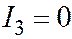 , , 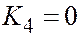 , , 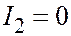 , , 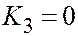 . . 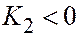 . .
| |
| 2 мн. пар. плоск. | 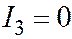 , , 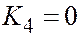 , , 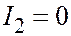 , , 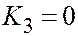 . . 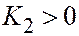 . .
| |
| 2 совпад. плоск. | 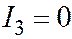 , , 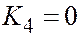 , , 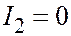 , , 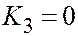 . . 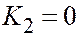 . .
|
Доказательство необходимости. Ранее было дока-зано, что если относительно ДПСК поверхность второго порядка задана общим уравнением (1), то преобразованием данной системы координат в другую, тоже Декартовую прямоугольную систему, общее уравнение (1) может быть преобразовано к одному из следующих 5 простейших видов:
I. 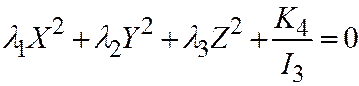 , если
, если 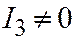 ;
;
II. 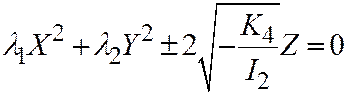 , если
, если 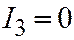 ;
; 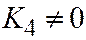 ;
;
III. 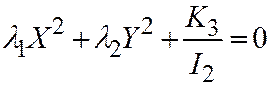 , если
, если 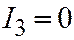 ;
; 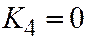 ;
; 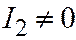
IV.  , если
, если 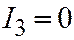 ;
; 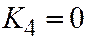 ;
; 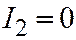 ;
; 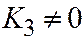 ;
;
V. 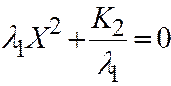 , если
, если 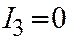 ;
; 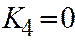 ;
; 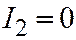 ;
; 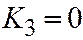 ;
; 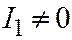 .
.
Во всех этих уравнениях 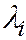 - отличные от нуля корни характеристического уравнения, а инварианты
- отличные от нуля корни характеристического уравнения, а инварианты  и
и  вычисляются по ранее указанным формулам.
вычисляются по ранее указанным формулам.
1. Если уравнение (I) является уравнением эллипсоида, то числа 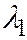 ,
, 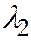 и
и 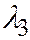 одного знака, а число
одного знака, а число 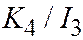 имеет знак, им противоположный. Но т.к.
имеет знак, им противоположный. Но т.к. 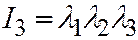 , то
, то 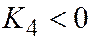 , и далее,
, и далее, 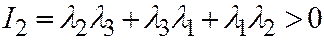 ,
, 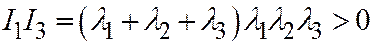 .
.
2. Если уравнение (I) является уравнением мнимого эллипсоида, то все числа 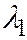 ,
, 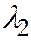 ,
, 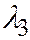 и
и 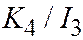 одного знака. Т.к.
одного знака. Т.к. 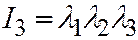 , то
, то 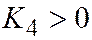 . Соотношения
. Соотношения 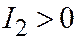 и
и 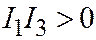 доказываются также, как в пункте 1.
доказываются также, как в пункте 1.
3. Если уравнение (I) является уравнением мнимого конуса, то 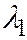 ,
, 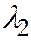 ,
, 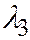 оного знака, а
оного знака, а 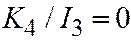 , откуда
, откуда 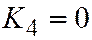 . А неравенства
. А неравенства 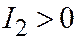 и
и 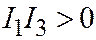 доказываются также, как в пункте 1.
доказываются также, как в пункте 1.
4. Если уравнение (I) является уравнением однополостного гиперболоида, то из чисел 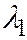 ,
, 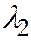 ,
, 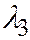 ,
, 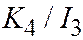 два положительны, а два отрицательны; если, например,
два положительны, а два отрицательны; если, например,  ,
, 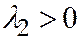 ,
, 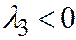 ,
, 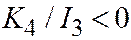 , то
, то 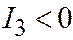 ,
, 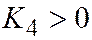 ; и, если например
; и, если например 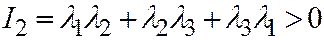 , то
, то 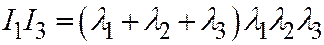 имеет знак, противоположный знаку
имеет знак, противоположный знаку 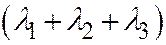 . Докажем, что
. Докажем, что 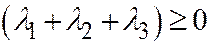 . (тогда
. (тогда 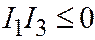 ). В самом деле, если бы мы имели
). В самом деле, если бы мы имели 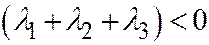 , то
, то 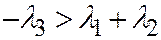 ,
, 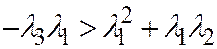 ,
, 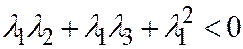 и
и 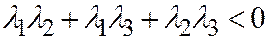 вопреки предположению. Тот же результат (
вопреки предположению. Тот же результат ( 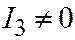 ,
, 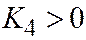 или
или 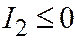 или
или 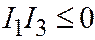 ) получим, предположив, что
) получим, предположив, что  ,
, 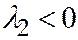 ,
, 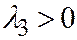 ,
, 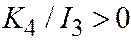 .
.
5. Если уравнение (I) является уравнением двуполостного гиперболоида, то два из корней 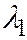 ,
, 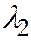 ,
, 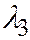 имеют одинаковый знак с
имеют одинаковый знак с 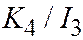 , а третий корень - знак, им противоположный. Пусть, например,
, а третий корень - знак, им противоположный. Пусть, например,  ,
, 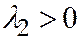 ,
, 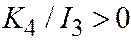 ,
, 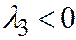 . Тогда
. Тогда 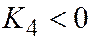 ;
; 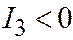 , а то, что или
, а то, что или 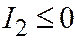 , или
, или 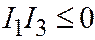 доказывается также, как в пункте 4.
доказывается также, как в пункте 4.
6. Если уравнение (I) является уравнением конуса второго порядка, то 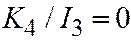 , откуда
, откуда 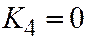 ,
, 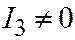 , и, далее, два из корней
, и, далее, два из корней 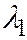 ,
, 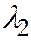 ,
, 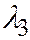 имеют одинаковый знак, а третий корень - знак, им противоположный. Отсюда, как и в случае 4, доказывается, что или
имеют одинаковый знак, а третий корень - знак, им противоположный. Отсюда, как и в случае 4, доказывается, что или 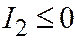 , или
, или 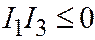 .
.
Перейдём к исследованию поверхностей второго порядка II группы.
7. Если уравнение II является уравнением эллиптического параболоида, то 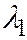 , и
, и 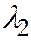 в уравнении II - числа одного знака, а это значит, что
в уравнении II - числа одного знака, а это значит, что 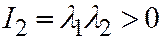 и из уравнения II следует, что
и из уравнения II следует, что 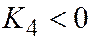 (число
(число 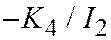 под радикалом в уравнении II положительно).
под радикалом в уравнении II положительно).
8. Если же уравнение II является уравнением гиперболического параболоида, то 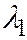 , и
, и 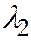 в уравнении II - числа разных знаков, а это значит, что
в уравнении II - числа разных знаков, а это значит, что 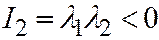 и из условия
и из условия 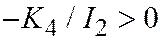 находим:
находим: 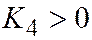 .
.
Рассмотрение остальных случаев по существу не отличается от выше доказанных.
Достаточность всех признаков доказывается методом от противного т.к. эти признаки взаимно исключают друг друга.
Результаты всех исследований помещены в табл. 3.
| <== предыдущая лекция | | | следующая лекция ==> |
| Организационные структуры государственной системы обеспечения информационной безопасности федеральных органов исполнительной власти | | | Корпоративная нормативная база по защите информации |
Дата добавления: 2016-04-14; просмотров: 846;
