Б.5 Аксиома затвердения
Условия равновесия сил, приложенных к абсолютно твердому телу, должны выполняться и для сил, которые прикладываются к деформированному телу. Однако, эти условия – необходимые, но не достаточные.
Например. Силы, приложенные к нити АВ (рис. Б.5), удовлетворяют условию равновесия при наличии условия, что они растягивают нить, а не сжимают ее.

Рисунок Б.5
Дополнение В
НЕКОТОРЫЕ ПРИМЕРЫ ИЗ ТЕХНИКИ, В КОТОРЫХ ИМЕЮТ МЕСТО СИЛЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
Пример 1.
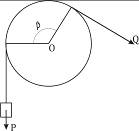 Рисунок В.1
Рисунок В.1
| Трос огибает неподвижный горизонтальный цилиндр (рис. В.1), к нижнему его концу прикреплен груз Р. Какое усилие нужно приложить ко второму концу троса, чтобы груз на упал, если угол обхвата равен β, а коэффициент трения троса о цилиндр равен f? |
Решение.
Эту классическую задачу решил впервые Леонард Эйлер*. По формуле Эйлера 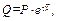 где е – основание натурального логарифма; f – коэффициент трения о цилиндр; β – угол охвата тросом цилиндра.
где е – основание натурального логарифма; f – коэффициент трения о цилиндр; β – угол охвата тросом цилиндра.
Анализируя формулу, видим, что сила Q не зависит от радиуса цилиндра, а зависит от параметров f и β. Сила Q уменьшается при увеличении угла β по закону показательной функции.
Пример 2.
| Какими должны быть размеры механизма L и l, изображенного на рисунке В.2, чтобы при известном коэффициенте трения скольжения (f = 0,6) между стеной и ползунами А и В механизм был самозаторможенным? |  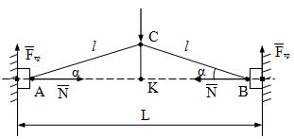 Рисунок В.2 Рисунок В.2
|
Решение.
Реакция шероховатой стенки на ползуны состоит из нормальной составляющей 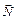 и силы трения
и силы трения 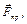
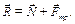
Как известно, равновесие ползуна на стене возможно тогда, когда силы пересекаются внутри угла трения, то есть реакции невесомых стержней должны быть направлены под такими углами α, чтобы 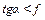 .
.
Из геометрических соображений имеем:
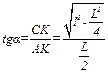 ,
, 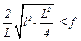 – ответ.
– ответ.
Для случая, когда f = 0,6 имеем 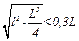 . Решая это неравенство,
. Решая это неравенство,
имеем:
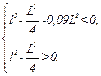
Удовлетворяют этой системе неравенств такие ограничения на геометрические параметры конструкции 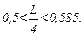
Пример 3.
| Определить наименьшее расстояние х (рис. В.3) центра тяжести груза весом Р от оси СС' платформы Е при котором груз с платформой будет находиться в равновесии, если коэффициент трения движущегося вертикального стержня о направляющие стойки А и В равен f (весом платформы пренебрегаем, d – диаметр движущегося стержня, h - расстояние между опорными точками стойки А и В). | 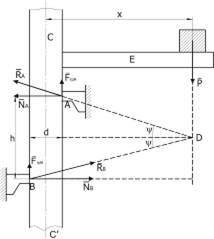 Рисунок В.3
Рисунок В.3
|
Решение.
За объект изучения берем конструкцию СС'Е, которая состоит из стержня и платформы. К ней приложены силы: 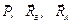 . Реакции в точках А и В в предельном состоянии направлены под известным углом трения
. Реакции в точках А и В в предельном состоянии направлены под известным углом трения 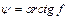 к горизонту. По теореме о трех непараллельных силах (п. 2.3), линии действия трех сил
к горизонту. По теореме о трех непараллельных силах (п. 2.3), линии действия трех сил 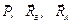 должны пересекаться в одной точке (в точке D).
должны пересекаться в одной точке (в точке D).
Составим уравнения равновесия произвольной плоской системы сил по формулам (5.5)
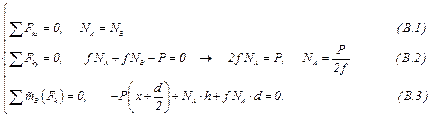
Из формулы (В.3) 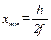 – ответ.
– ответ.
Чем меньше коэффициент трения, тем больше расстояние х. На свойствах самоторможения, которые имеют место в этих примерах, базируются строительные устройства и другие механизмы.
Пример 4.
Радиус цапфы меньше радиуса круга подшипника (рис. В.4). Цапфа нагружена силой 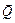 и некоторой парой, момент которой равен m. Чтобы цапфа не вращалась, а находилась в равновесии найти условие, которому должны удовлетворять: коэффициент трения скольжения f, момент m, сила и некоторой парой, момент которой равен m. Чтобы цапфа не вращалась, а находилась в равновесии найти условие, которому должны удовлетворять: коэффициент трения скольжения f, момент m, сила 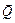 , радиус цапфы r. , радиус цапфы r.
| 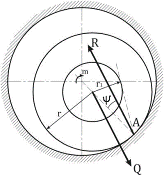 Рисунок В.4
Рисунок В.4
|
Решение.
Трением качения пренебрегаем. Из-за того, что пару сил можно уравновесить только парой сил, точка приложения реакции опоры на цапфу 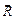 должна находиться на определенном расстоянии от линии действия силы
должна находиться на определенном расстоянии от линии действия силы 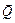 . Пара сил
. Пара сил 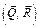 будет уравновешивать пару сил с моментом m. Обозначим ψ – угол, который образует реакция
будет уравновешивать пару сил с моментом m. Обозначим ψ – угол, который образует реакция 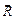 с нормалью к контактирующим поверхностям в точке А. Тогда составим уравнения равновесия параллельной плоской системы сил (формула (5.8))
с нормалью к контактирующим поверхностям в точке А. Тогда составим уравнения равновесия параллельной плоской системы сил (формула (5.8))
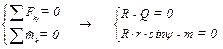
Откуда 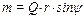 . При этом ψ ≤ φ, где φ – угол трения,
. При этом ψ ≤ φ, где φ – угол трения, 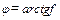 . То есть
. То есть 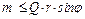 – ответ.
– ответ.
Вывод.
Если построить круг трения, радиус которого равен 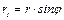 , то при равновесии реакция
, то при равновесии реакция 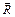 должна прикасаться, или пересекать круг трения.
должна прикасаться, или пересекать круг трения.
Дополнение Г
Дата добавления: 2016-03-15; просмотров: 988;
