РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ СТАТИКИ. ПРИВЕДЕНИЕ
ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К БОЛЕЕ ПРОСТОМУ ВИДУ
(к теме 6)
Рассмотрим несколько задач статики твердого тела на тему «Приведение произвольной пространственной системы сил к более простому виду». Задачи на эту тему рекомендуется решать по следующему алгоритму:
1) выбираем систему координат так, чтобы большинство сил были параллельны или перпендикулярны к выбранным осям, а линии действия сил пересекали эти оси;
2) за центр приведения выбираем начало координат, точку О;
3) определяем проекции главного вектора и главного момента относительно точки О по формулам (Е.1) и (Е.2), соответственно:
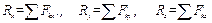 ; (Е.1)
; (Е.1)
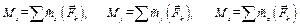 ; (Е.2)
; (Е.2)
4) определяем модули главного вектора и главного момента относительно точки О по формулам (Е.3) и (Е.4), соответственно:
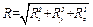 , (Е.3)
, (Е.3)
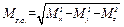 ; (Е.4)
; (Е.4)
5) в зависимости от величин главного вектора и главного момента, а также от значения второго инварианта статики 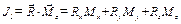 , выясняем, к чему приводится заданная система сил (пользоваться табл. 6.1).
, выясняем, к чему приводится заданная система сил (пользоваться табл. 6.1).
Пример 1.
Задана система сил: 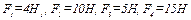 ,
которые приложены в точках,
указанных на рисунке Е.1. ,
которые приложены в точках,
указанных на рисунке Е.1.
| 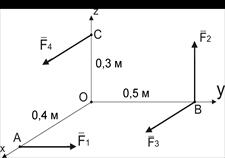 Рисунок Е.1
Рисунок Е.1
|
Решение.
Выберем систему координат, как показано на рис. Е.1. Найдем проекции и модуль главного вектора 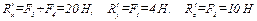
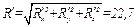 Н.
Н.
Найдены проекции главного момента на координатные оси.
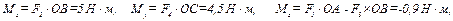
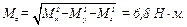
Имеем: 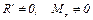 . Определим значение скалярного произведения
. Определим значение скалярного произведения 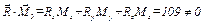 , то есть случай 5 (табл. 6.1).
, то есть случай 5 (табл. 6.1).
Ответ.
Система сил приводится к динамическому винту.
Пример 2. [4]
По трем ребрам параллелепипеда действуют три одинаковые по модулю силы 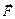 . Ребра имеют длины а, b, с
(рис. Е.2).
Каким должно быть соотношение между длиной ребер, чтобы система сил приводилась к равнодействующей? . Ребра имеют длины а, b, с
(рис. Е.2).
Каким должно быть соотношение между длиной ребер, чтобы система сил приводилась к равнодействующей?
| 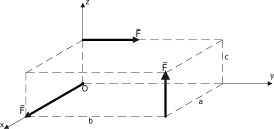 Рисунок Е.2
Рисунок Е.2
|
Решение.
Система координат выбрана на рисунке Е.2. Найдем проекции и модуль главного вектора 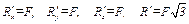 .
.
Найдем проекции главного момента относительно точки О на оси координат
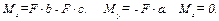
Модуль главного момента равняется
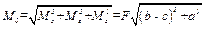 .
.
Система сил приводится к равнодействующей, если выполняется одно из условий (табл. 6.1), или МТ.О = 0, или 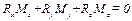 :
:
1) М0 = 0, то есть 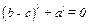 ;
;
2) 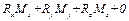 , то есть
, то есть 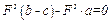 , b - c - a = 0.
, b - c - a = 0.
В первом случае: 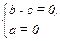 то есть b = c. Во втором случае: b = c + а.
то есть b = c. Во втором случае: b = c + а.
Дополнение Ж
Дата добавления: 2016-03-15; просмотров: 1232;
