И.2 Центр тяжести площади кругового сектора
Для определения центра тяжести сектора радиуса R с центральным углом 2α, разобьем его на элементарные секторы, как показано на рисунке И.2.
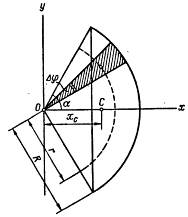 Рисунок И.2
Рисунок И.2
| Каждый из этих элементарных секторов можно рассматривать как треугольник, ведь дугу, которой ограничен этот сектор, из-за малости, можно рассматривать как прямолинейный отрезок. Центр тяжести такого треугольника находится в точке пересечения его медиан, то есть на расстоянии 2/3R от вершины. Следовательно, геометрическим местом центров тяжестей всех элементарных секторов является дуга круга радиуса r = 2/3R.
Найдя центр тяжести этой дуги, так же найдем центр тяжести площади кругового сектора. Применяя формулу (Е.4) для дуги радиуса r, получим 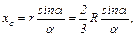
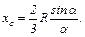 (И.6) (И.6)
|
Полученная формула определяет центр тяжести площади сектора радиуса R. В этой формуле α – половина центрального угла в радианах. В частном случае для полкруга ( 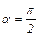 ) получим
) получим
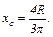 (И.7)
(И.7)
* Эйлер Леонард (1707 – 1783) – известный математик, родился в Швейцарии, з 1727 р. работал в Петербургской АН.
Дата добавления: 2016-03-15; просмотров: 1169;
