НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ГЛАВНОГО МОМЕНТА ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
(к теме 6)
Рассмотрим, как изменится главный момент системы сил 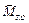 относительно произвольной точки О (рис. Д.1) при изменении положения этой точки по отношению к центральной оси.
Как известно (формула (6.12)), главный момент относительно точки О состоит из двух моментов относительно произвольной точки О (рис. Д.1) при изменении положения этой точки по отношению к центральной оси.
Как известно (формула (6.12)), главный момент относительно точки О состоит из двух моментов 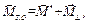 где согласно (6.13) и (6.14) где согласно (6.13) и (6.14)
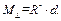 , (Д.1)
где , (Д.1)
где 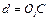 или или 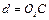
| 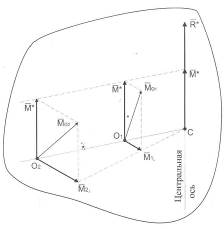 Рисунок Д.1
Рисунок Д.1
|
Модуль главного момента 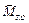 определяется формулой
определяется формулой
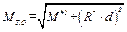 , (Д.2)
, (Д.2)
которая показывает, что при увеличении расстояния d от точки О до центральной оси, модуль главного момента увеличивается. Вместе с тем, растет его угол наклона к главному вектору. Направление главного момента 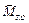 определяется углом α, косинус которого равняется
определяется углом α, косинус которого равняется
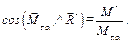 (Д.3)
(Д.3)
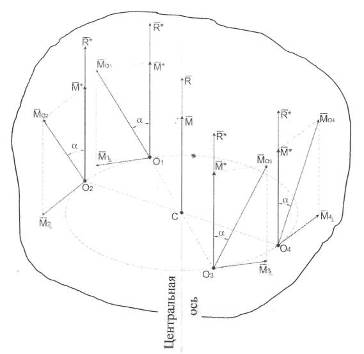
Если рассмотреть точки О1, О2, О3, О4 (рис. Д.2), которые находятся на одинаковом расстоянии от центральной оси, то согласно формулам (Д.2) и (Д.3), имеем: главные моменты системы сил относительно этих точек равны по модулю и образуют одинаковый угол α с направлением центральной оси. Этим и объясняется термин «центральная ось системы».
Главный момент имеет наименьшее значение (для d = 0) относительно точек центральной оси системы. Получим формулу для расчета наименьшего значения главного момента:
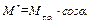 .
.
|
Рисунок Д.2
Умножим и разделим правую часть этой формулы на модуль главного вектора. Получим еще одну формулу для определения наименьшего значения главного момента пространственной системы сил
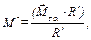
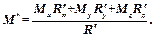 (Д.4)
(Д.4)
Дополнение Е
Дата добавления: 2016-03-15; просмотров: 1963;
