Закон равномерной плотности
К наиболее распространенным в природе законам распределения относят следующие: закон равномерной плотности, нормальный закон распределения, закон Пуассона и экспоненциальное распределение. Рассмотрим их более подробно.
Случайную непрерывную величину X называют распределенной равномерно на интервале (a, b), если ее плотность распределения на этом интервале постоянна, а вне этого интервала равна нулю.
Пусть случайная величина X может принимать частные значения от a до b, причем все частные значения равновероятны (Рис.7). Требуется определить выражение для плотности вероятности f(x).
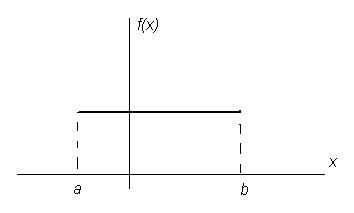
Рисунок 7 График плотности распределения случайной величины X
Для определения выражение для плотности вероятности f(x) воспользуемся свойством плотности распределения
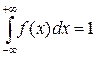 .
.
Поскольку по определению f(x) есть величина постоянная, то ее можно вынести за знак интеграла, т.е.
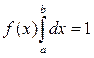 . Откуда
. Откуда 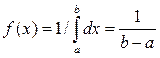 .
.
Зная выражение для плотности вероятности f(x), можно найти функцию распределения как
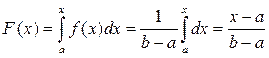 .
.
График функции равномерного распределения в соответствии с этим выражением примет вид, изображенный на рис.8.
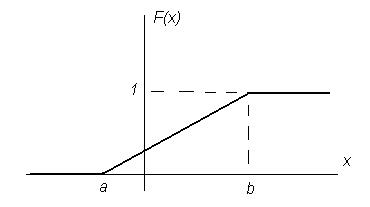
Рисунок 8 График функции равномерного распределения
При известном выражении для плотности равномерного распределения нетрудно вывести выражения, позволяющие вычислить математическое ожидание, дисперсию и средне - квадратичное отклонение для этого закона
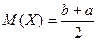 ;
; 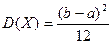 ;
; 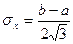 .
.
Дата добавления: 2016-04-19; просмотров: 1690;
