Композиция нормального и равномерного распределений

Пусть случайная величина X подчинена нормальному закону с плотностью распределения

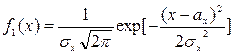, а случайная величина Y распределена равномерно в интервале [a, b]: . Требуется найти плотность распределения композиции случайных величин X и Y.

Решение.

Применяя формулу (4.14), получим

.

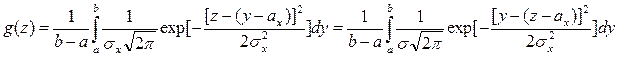Подынтегральная функция есть плотность нормально распределенной случайной величины Y, а интеграл представляет собой вероятность попадания случайной величины в промежуток [a, b].

Следовательно,

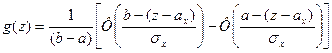. (4.17)

Если выполняется неравенство

, то выражение (4.17) можно отнести к нормальному распределению:

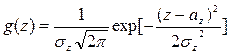, где ,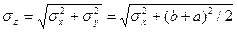

.

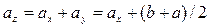Понятие о центральной предельной теореме Ляпунова

Если случайные величины взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием 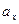и дисперсией 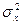, то при неограниченном увеличении n закон распределения суммы 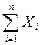неограниченно приближается к нормальному закону:

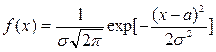с параметрами и .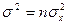

Теорема Ляпунова верна и для суммы случайных величин с неодинаковыми законами распределения, 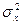у которых дисперсии примерно одного порядка.