ЗАДАЧА 5. ИЗУЧЕНИЕ ДИФРАКЦИОННОЙ РЕШЕТКИ С ПОМОЩЬЮ ГОНИОМЕТРА

Явление дифракции состоит в отклонении света от прямолинейного распространения вблизи непрозрачных препятствий, размеры которых сравнимы с длиной световой волны.

Дифракция света обусловлена взаимодействием световых волн с краями препятствий. Решение задачи дифракции сводится к нахождению распределения освещенности на экране в зависимости от размеров и форм препятствий. Строгое математическое решение такой задачи на основе электромагнитной теории Максвелла является сложным, однако оно может быть сведено к принципу Гюйгенса-Френеля.

Дифракционная решетка представляет собой стеклянную или метал­лическую пластинку, на которой с помощью делительной машины через строго одинаковые интервалы нанесены параллельные штрихи. Обычно применяемые в лабораторных условиях решетки являются отпечатками таких гравированных решеток (реплики); они изготовляются из специ­альной пластмассы. Основными параметрами решетки являются период d (иначе постоянная решетки ) и число штрихов N.

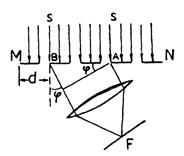
Дифракционные решетки обычно применяются в таких условиях, ко­гда имеет место дифракция Фраунгофера, т.е. когда на решетку падает плоская волна, а точка наблюдения практически находится в бесконеч­ности. В этом случае положение точки наблюдения определяется углом j между нормалью к решетке и направлением лучей (рис.1).

Распределение интенсивности в дифракционной картине опреде­ляется суперпозицией волн, при­ходящих в точку наблюдения от разных щелей решетки. При этом амплитуды всех интерферирующих волн при заданном угле j прак­тически одинаковы, а фазы составляют арифметическую прогрессию. Интенсивность дифрагированного света максимальна для таких углов j_m, для которых колебания, приходящие от всех щелей, оказы­ваются в фазе.

Пусть на решетку MN (рис.1) падает нормально пучок монохро­матических световых лучей. Возьмем два симметричных луча SA и SB. Согласно принципа Гюйгенса точки A и B можно рассматриватькак центры вторичных световых колебаний, распространяющихся во все стороны, поэтому лучи их можно наблюдать под углом j к падающему. Разность хода между двумя лучами, идущими от соседних щелей под уг­лом j к первоначальному направлению лучей, будет равна ВС. Если ВС равно четному числу полуволн (т.е. лучи приходят в точку наблюдения в фазе), то в точке наблюдения будет максимум светового эффекта. Если же ВС равно нечетному числу полуволн, то в точке наблюдения будет минимум интенсивности света. Свяжем величину ВС с параметрами решетки и длиной световой волны. Из DАВС следует, что BC = AB×sinj = d ×sinj, где d – постоянная решетки, т.е., сумма прозрачной части щели и непрозрачной царапины. Для наблюдения максимума освещенности должно выполняться условие

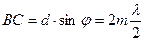, т.е. 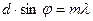(1)

где m = 1, 2, 3, . . . означает порядок светового максимума.

При этом интенсивность света, распространяющегося под углом j к нормали решетки, определяется выражением:

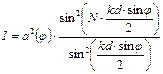(2)

где k = 2p / l волновое число, а множитель a²(j) учитывает интерференцию волн, испускаемых одним "периодом" решетки.

Как следует из (1), углы дифракции, для которых наблюдаются све­товые максимумы, зависят от l. Дифракционная решетка представляет собой, таким образом, спектральный прибор. Если на решетку падает свет сложного спектрального состава, то после нее образуется спектр, причем фиолетовые лучи отклоняются решеткой на меньшие углы, чем красные. При m = 0 максимумы интенсивности для всех длин волн накла­дываются друг на друга, так как для всех l j = 0. Поэтому при осве­щении решетки белым светом максимум нулевого порядка является не­окрашенным. Спектры первого, второго и т.д. порядков (в которых повторяется одно и то же чередование цветов) располагаются симме­трично по обе стороны от нулевого.

Рассмотрим основные характеристики дифракционной решетки.

1. Угловая дисперсия D характеризует угловое расстояние между двумя близкими спектральными линиями

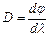(3)

Из (1) следует, что

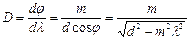(4)

Как видно из (4), дисперсия зависит от порядка спектра.

2. Разрешающая способность. Для любого спектрального прибора разрешающая способность характеризует возможность разделения двух близких спектральных линий. В случае дифракционной решетки она за­висит от общего числа штрихов решетки и определяется выражением

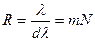(4)

Спектральный интервал dl, входящий в это выражение, характеризует минимальное расстояние между двумя спектральными линиями, которые еще могут быть разрешены данной дифракционной решеткой.

3. Дисперсионная область. При достаточно широком спектральном интервале падающего света получаемые с помощью решетки спектры различных порядков начинают перекрываться. Предельная ширина спек­трального интервала Dl, при которой наложения спектров ещё не происходит, называется дисперсионной областью. Для решетки

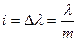(6)

Целью данной работы является следующее.

1. Получить с помощью дифракционной решетки спектр излучения ртути и измерить длины волн всех видимых спектральных линий (не менее 6). Измерения провести для 2 – 3 порядков.

2. Известно, что при косом падении пучка лучей на решетку дифракционная картина получается такой, как если бы мы взяли другую ре­шетку с меньшим периодом. Поставить решетку под произвольным углом (~45°) к падающему пучку лучей и определить новый период решетки, используя значения l, полученные в задании 1.

3. Определить угловую дисперсию, дисперсионную область и разрешающую способность исследуемой решетки.

Для выполнения работы необходимо измерить углы дифракции для различных длин волн. Такие измерения проводятся с помощью гониометра-спектрометра ГС-5, с устройством которого знакомятся перед вы­полнением работы.

Порядок выполнения работы.

1. Расположить перед щелью коллиматора ГС-5 источник ртутного спектра.

2. Зрительную трубу гониометра установить так, чтобы щель колли­матора была четко видна и нить окуляра проходила через середину щели. Ширину щели взять в пределах 0,1 ¸ 0,3 мм.

3. Закрепить на середине столика гониометра дифракционную ре­шетку (перпендикулярно к оптической оси коллиматора либо под уг­лом к ней – в зависимости от задания).

4. Навести нить зрительной трубы на первую цветную линию слева от максимума нулевого порядка и сделать отсчет по лимбу зрительной трубы j₁'. Затем установить зрительную трубу на следующие линии и сделать для них отсчеты j₂', j₃' и т.д. Замерив положение всех линий в пределах первого порядка, перейти к определению поло­жения линий в пределах второго порядка и т.д. (количество порядков, для которых необходимо сделать измерения, указывается преподава­телем).

5. Провести аналогичные измерения для линий тех же цветов в ука­занных порядках спектров, расположенных вправо от нулевого макси­мума. Положения зрительной трубы в этом случае будут j₁", j₂", j₃" и т.д.

Очевидно, разность j_i' – j_i", где j_i' и j_i" – положения зрительной трубы, наведенной слева и справа от нулевого максимума на линию одного и того же цвета, соответствующие одному и тому же порядку, дает нам двойной угол дифракции для данной спектральной линии. Таким образом, j_i = (j_i' – j_i") / 2.

6. Определив j_i, рассчитать по формуле (1) длины волн всех про­меренных спектральных линий. Для одних и тех же цветов значения l, полученные для различных порядков спектра, усреднить и определить погрешность измерения длины волны. Указанные измерения провести при выполнении заданий 1 и 2.

7. Для определения угловой дисперсии решетки нужно измерить уг­ловое расстояние между двумя близкими спектральными линиями. Для этой цели удобно использовать желтые линии ртути. Измерения надо проводить в спектрах различных порядков. Результаты опыта (с исполь­зованием формулы (3)) сопоставить с расчетными данными, получен­ными из соотношения (4).

8. Определить ширину спектральной области решетки. Как следует из (6), ширина дисперсионной области уменьшается с увеличением по­рядка спектра. Рекомендуется проделать следующее: осветить щель коллиматора лампой накаливания и с помощью зрительной трубы наблюдать сплошной спектр в разных порядках. Определить порядок спектра, начи­ная с которого соседние спектры перекрываются. По формуле (6) определить I.

Литература: 1 – 4.