ЗАДАЧА 3. ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА.

Согласно теории, резкие интерференционные картины будут иметь место лишь при точечных источниках света. На практике условие точечности источника осуществляется лишь приближенно, а во многих случа­ях совсем не выполняется. Чаще всего при явлениях интерференции нам приходится иметь дело с протяженными источниками, наблюдаемыми в естественных условиях. Весьма важный случай подобного рода имеет место при освещении тонких прозрачных пленок, когда необходимое для возникновения двух когерентных пучков расщепление световой волны происходит вследствие отражения света на передней и задней поверх­ностях пленки.

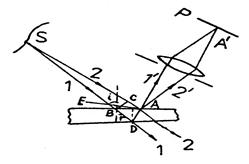Если пленка имеет клинообразную форму, интерференционная карти­на локализована на поверхности клина (возникают полосы равной тол­щины.) Условия формирования интерференционной картины вблизи поверх­ности таких пленок можно выяснить, рассмотрев схему опыта, представ­ленного на рис.1.

Рис.1. Ход лучей при интерференции плоской волны в оптическом клине

Пусть на поверхность тонкого прозрачного клина с показателем преломления n падают почти нор­мально световые пучки от протяжен­ного источника света. Когерентными являются световые волны, излучаемые одной точкой источника. Проведем для начала расчет интерференции световых пучков, излучаемых одной точкой протя­женного источника света. Разность хо­да D когерентных световых пучков 1’ и 2’ необходимо вычислять в точке A на поверхности клина, в месте локализации интерференционных полос. В ходе расчета надо также учесть, что луч, испытывающий отражение на границе раздела "менее плотная – более плотная среда", изменяет скачком свою фазу на p, что равносильно изменению оптического пути луча на l/2. Как видно из рис.1,

;

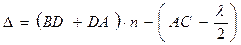
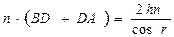
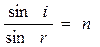
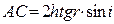Здесь h = ED – толщина клина. Отсюда

(1)

Полученное значение разности хода D является функцией h и r. Но обычно r изменяется в малых пределах, поэтому можно счи­тать, что D оказывается только функцией толщины клина в точке A.

Из выражения (1) следует, что при малых вариациях углов i (и, соответственно, r) разность хода D световых пучков, излучаемых и другими точками протяженного источника света, будет в точке A прибли­зительно такой же, как и для рассмотренных пучков 1’ и 2’. Следова­тельно, в точке A на поверхности клина интерференционные картины, созда­ваемые различными парами световых лучей, приходящими от разных то­чек светящейся поверхности источника, будут приблизительно совпа­дать между собой. Отсюда вытекает высокая видимость интерференцион­ной картины на поверхности клина.

Особый интерес представляет случай интерференции в тонком воз­душном слое, известный под названием колец Ньютона. Эта картина на­блюдается, когда выпуклая поверхность линзы малой кривизны сопри­касается в некоторой точке с плоской поверхностью хорошо отполи­рованной пластинки так, что остающаяся между ними воздушная прос­лойка имеет форму клина. Если на такую систему (приблизительно нормально к поверхности пластинки) падает пучок монохроматическо­го света, то световые волны, отраженные от верхней и нижней границ этой воздушной прослойки, интерферируют между собой. (Ход интерфе­рирующих лучей для этого случая показан на рис.2. Преломлением при прохождении лучей через границу "нижняя поверхность линзы - воздушный зазор" пренебрегаем, т.к. угол падения мал за счет малой кривизны линзы.) Возникающая интерференционная картина имеет следую­щий вид: в точке соприкосновения - темное пятно, оно окружено рядом концентрических светлых и черных колец убывающей ширины.

Наблюдение колец Ньютона является одним из наиболее простых методов изуче­ния интерференции и определения длины l световой волны. Нетрудно рассчитать размеры и положение колец Ньютона при нормальном падении света на по­верхность пластинки. В этом случае D = 2h×cosr + l/2 = 2h + l/2, так как cosr = 1 и n = 1, Согласно теории, интерферирующие лучи усиливают друг друга, если D = 2k×l/2, и ослабляют при D = (2k + 1)×l/2, где k – целое число (порядок максимума или минимума). Поэтому в точке соприкосновения линзы с пластинкой, где h = 0, D = l/2, мы будем наблюдать минимум. Для других точек D = 2h + l/2 и кольцо будет светлое, если D = 2k×l/2, или темное при D = (2k + 1)×l/2. Из сказанного видно, что минимум будет при 2h = kl. Величина h может быть выражена через радиус кривизны линзы и радиус темного интерференционного кольца r_k. Действительно, из рис.2 следует, что r_k² = (2R - h)×n, где R – радиус кривизны линзы. Если h мало по сравнению с R, то r_k² = 2Rn, и тогда l = r_k² / kR. Однако эта формула может давать значительную погрешность при вычислении l вследствие того, что зазор между линзой и пластинкой нельзя свести к нулю. Если он равен d, то это приводит к возникновению дополнительной разности хода в 2d. Тогда условие образования темных колец примет вид 2h + l/2 + 2d = (2k + 1)×l/2 или h = kl/2 – d, и для радиуса k-того темного кольца получим

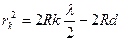
Величина d не может быть измерена непосредственно, но ее можно исключить. Для кольца m-того порядка r_m² = 2Rm×l/2 – 2Rd. Взяв разность r_m² – r_k², получим r_m² – r_k² = R(m – k)×l, откуда

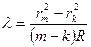(2)

Таким образом, зная радиус кривизны линзы и радиусы темных интерференционных колец, можно вычислить длину световой волны l.

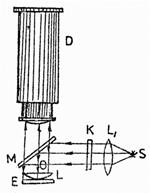Для выполнения работы используется установка, схема которой изо­бражена на рис.3. Здесь S – источник света (лампочка накаливания), К – светофильтр, пропускающий свет, длина волны которого подлежит измерений, L₁ – плосковыпуклая линза, Е – стеклянная пластинка, D – микроскоп с окулярной шкалой, цена деления которой указывается. Монохроматические лучи, проходя через линзу L₁, попадают через линзу L, на пластинку Е, отражаются и интерферируют. Интерференцион­ная картина рассматривается в микроскоп, при этом она будет видна в увеличенном масштабе.

Работа выполняется в следующем порядке.

1. Вращая барабан окулярного микрометра, устанавливают его крест на какое-либо, достаточно удаленное от центра, темное коль­цо, например, 12-ое слева, и производят отсчет по шкале и барабану микрометра, повторяют измерение положения одного и того же кольца несколько раз и нахо­дит среднее значение. Затем, перемещаясь вдоль диаметра, крест микрометра последовательно наводят на 11-ое, 10-ое и т.д. кольца и про­изводят отсчеты. Пройдя центральное пятно, снимают показания для тех же колец вправо от центра интерференционной картины. (Несколь­ко ближайших к центру колец обычно бывают сильно размыты. Это за­трудняет достаточно точное определение их радиусов, поэтому изме­рение их положения можно не производить.)

2. Определяют радиусы измеренных колец. Очевидно, что радиус k-того кольца r_k = 1/2(x_2k – x_1k)×i, где x_2k, x_1k – отсчеты по шкале микромет­ра справа и слева, i - цена деления шкалы.

3. Комбинируя попарно радиусы колец, по формуле (2) определяют длину волны падающего света. При этом рассчитывают не менее пяти комбинаций.

4. Определяют среднее значение длины волны и ошибку в её определении.

5. Проводят указанные измерения для нескольких фильтров, указан­ных преподавателем, и сравнивают точность в определении l для различных участков спектра.

6. Обработку результатов измерений проводят также графическим методом. Очевидно, если построить график зависимости r_k² от номеров колец, то получим прямую линию. угол наклона которой позволяет най­ти l, так как tga = lR. Определить l из графической зависи­мости. Сравнить данные, полученные обоими методами, и указать, какой метод вычисления длины волны более точен.

Литература: 1, 2, 4.