Аналитическое выравнивание по уравнению гиперболы
Если для динамического ряда характерны затухающие абсолютные снижения уровней (например, динамика трудоемкости продукции, трудообеспеченности производства в сельском хозяйстве и др.), то выравнивание в таких случаях наиболее целесообразно проводить по уравнению гиперболы, т.е.
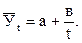 (9.38)
(9.38)
При этом порядок нахождения параметров а, в, и расчет уровней динамического ряда аналогичен применению приема выравнивания показателей по уравнению прямой линии. При условии 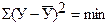 система нормальных уравнений принимает следующий вид:
система нормальных уравнений принимает следующий вид:
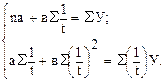
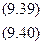
В качестве примера аналитического выравнивания по уравнению гиперболы возьмем динамический ряд трудоемкости молока в фермерском хозяйстве «Нива» за 2006 – 2010 гг. (табл.9.12).
Т а б л и ц а 9.12.Выравнивание трудоемкости молока по уравнению
Гиперболы
| Годы | Фактическая трудоемкость, 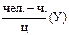
| Расчетные величины | Выравненная трудоемкость, 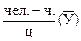
| |||
| t | 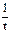
| 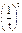
| 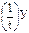
| |||
| 1,00 | 1,00 | 12,0 | 12,1 | |||
| 0,50 | 0,25 | 5,0 | 9,6 | |||
| 0,33 | 0,10 | 3,0 | 8,7 | |||
| 0,25 | 0,06 | 2,0 | 8,4 | |||
| 0,20 | 0,04 | 1,6 | 8,2 | |||
| Итого | - | 2,28 | 1,45 | 23,6 |
Параметры а, в уравнений (9.39 и 9.40) можно найти путем решения системы уравнений:
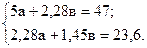
Отсюда 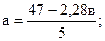
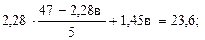
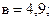
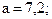
Уравнение гиперболы для выравнивания динамики трудоемкости молока в фермерском хозяйстве примет следующий вид:
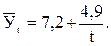 (9.41)
(9.41)
Подставляя в уравнение 9.41 соответствующие значения t, находим выровненные уровни 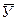 , например:
, например:
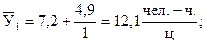
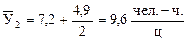 и т.д.
и т.д.
Таким образом, получаем варавненный по уравнению гиперболы динамический ряд трудоемкости молока в фермерском хозяйстве «Нива» (табл. 9.12).
Правильность расчетов по аналитическому выравниванию динамического ряда с применением любого способа проверяется совпадением суммы фактических и суммы выравненных уровней, т.е. 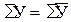 .
.
Дата добавления: 2016-02-20; просмотров: 1190;
