Форма записи формул логики предикатов
Рассмотрим предикат P(x), для него верны формулы пронесения отрицания через кванторы:
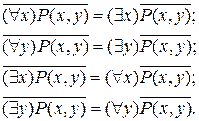
Предикатная формула находится в приведенной форме, если в ней использованы только кванторные операции, а также операции инверсии, конъюнкции, дизъюнкции, причем инверсия относится только к предикатным буквам.
Предикатная формула находится в предваренной форме (предваренной нормальной форме), если она имеет вид 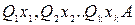 , где
, где 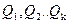 – кванторы всеобщности или существования, а формула A находится в приведенной форме и не содержит кванторов.
– кванторы всеобщности или существования, а формула A находится в приведенной форме и не содержит кванторов.
Пример 1.Записать формулу А в предваренной нормальной форме:
A = 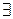 x
x 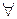 y P(x, y) →
y P(x, y) → 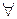 x
x 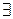 y Q(x, y)
y Q(x, y) 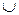 R(x).
R(x).
Решение:
A = 
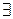 x
x 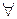 y P(x, y)
y P(x, y) 
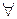 x
x 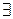 y Q(x, y)
y Q(x, y) 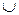 R(x) =
R(x) =
= 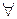 x
x 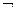
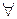 y P(x, y)
y P(x, y) 
 x
x  y Q(x, y)
y Q(x, y) 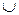 R(x) =
R(x) =
= 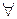 x
x 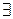 y
y 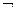 P(x, y)
P(x, y) 
 x
x  y Q(x, y)
y Q(x, y) 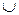 R(x).
R(x).
Полученная формула записана в приведенной форме. Для того чтобы квантор всеобщности можно было вынести за скобки, переобозначим переменные и выполним преобразования:
A =  t
t  y
y 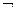 P(t, y)
P(t, y) 
 z
z  y Q(z, y)
y Q(z, y)  R(x) =
R(x) =
=  t(
t(  y
y 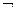 P(t, y)
P(t, y) 
 z
z  y Q(z, y)
y Q(z, y)  R(x)) =
R(x)) =
=  t
t  z (
z (  y
y 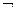 P(t, y)
P(t, y) 
 y Q(z, y)
y Q(z, y)  R(x)) =
R(x)) =
=  t
t  z
z  y(
y( 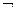 P(t, y)
P(t, y) 
 y Q(z, y)
y Q(z, y)  R(x)) – предваренная форма.
R(x)) – предваренная форма.
Пример 2.Записать формулу в предваренной нормальной форме: 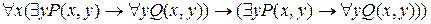 .
.
Решение:
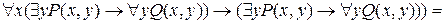
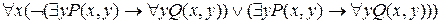 = =
= = 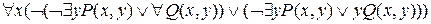 =
=
= 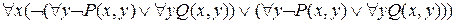 =
=
= 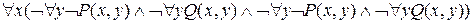 =
=
= 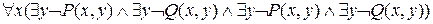 =
=
= 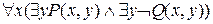 =
=
= 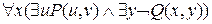 =
= 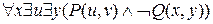 .
.
Это преобразование предназначено для исключения из предикатных формул кванторов существования при сохранении семантики.
Рассмотрим формулу 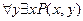 , поскольку квантор существования находится внутри области действия квантора всеобщности, допускается, что х, который «существует», может зависеть от значения у. Пусть эта зависимость определяется явно с помощью некоторой функции f(у), отображающей каждое значение у в х, который существует. Такая функция называется функцией Сколема. С её помощью формула примет вид
, поскольку квантор существования находится внутри области действия квантора всеобщности, допускается, что х, который «существует», может зависеть от значения у. Пусть эта зависимость определяется явно с помощью некоторой функции f(у), отображающей каждое значение у в х, который существует. Такая функция называется функцией Сколема. С её помощью формула примет вид 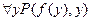 .
.
Общее правило исключения из предикатной формулы квантора существования состоит в замене всюду в ней переменной, относящейся к квантору существования, функцией Сколема, аргументами которой служат переменные, относящиеся к тем кванторам всеобщности, области действия которых охватывают область действия исключаемого квантора существования. Функции Сколема не должны совпадать с теми буквами, которые уже имеются в формуле.
Пример. Приведем к сколемовской форме формулу 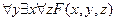 .
.
Приоритетность действий кванторов, имеющихся в префиксной форме представления, определяются слева направо, следовательно:
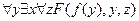 .
.
Аналогично 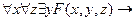
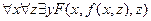 ;
;
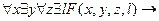
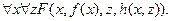
Если переменная, связанная квантором существования, является крайней слева, то она заменяется на константу.
Если подобным образом исключить связанные квантором существования переменные, то любые другие переменные, которые встречаются в формуле, будут связаны только квантором всеобщности и поэтому уже не понадобится пояснять это обстоятельство связыванием переменных кванторами. Иначе говоря, так как порядок расположения кванторов всеобщности несущественен, то можно эти кванторы явным образом не указывать (то есть опустить). Такое формальное представление предикатных формул называют сколемовской нормальной формой.
Любое выражение, записанное в СКНФ, можно представить в виде конъюнкции конечного множества дизъюнкций предикатов и (или) их отрицаний. Для этого необходимо к СКНФ несколько раз применить правило
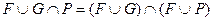 .
.
Клаузальной формой называется часть сколемовской формы, ограниченная скобками (часть предикатов, связанных дизъюнкцией). Если, например, если сколемовская форма имеет вид:
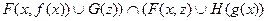 ,
,
то части формулы, соединенные конъюнкцией, образуют множество:
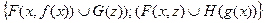 .
.
Таким образом, КНФ исходной формулы можно разложить на предложения. Множество предложений, полученных в результате разложения, называется клаузальным множеством. Поскольку любое предложение совершенно независимо от всех других, то между этими предложениями отсутствуют какие-либо взаимосвязи. Поэтому в общем нельзя говорить об эквивалентности формулы логики предикатов и клаузального множества.
Упражнения
Записать инверсию формул в предваренной нормальной форме:
1)  xA(x);
xA(x);
2)  x(A(x)B(x));
x(A(x)B(x));
3)  xA(x);
xA(x);
4)  x(A(x) →
x(A(x) →  yB( y));
yB( y));
5)  x(A(x)B(x)C(x));
x(A(x)B(x)C(x));
6)  x(A(x) → B(x));
x(A(x) → B(x));
7)  x(A(x) ↔ B(x));
x(A(x) ↔ B(x));
8)  x(A(x)
x(A(x) 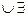 yB( y));
yB( y));
9)  x(A(x) → B(x))
x(A(x) → B(x)) 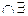 x(C(x)
x(C(x)  D(x));
D(x));
10)  x
x  y
y  z(A(x, y, z) → B(x, y, z)).
z(A(x, y, z) → B(x, y, z)).
Дата добавления: 2016-04-11; просмотров: 3411;
