Вывод в исчислении высказываний
Формальная система, порождающая высказывания, которые являются тавтологиями и только их, называются исчислением высказываний (ИВ).
Все логические законы должны быть тавтологиями (тождественно истинными). Иногда законы называются правилами вывода, которые определяют правильный вывод из посылок:
1) Modus ponens (правило отделения) 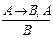 ;
;
2) Формальная запись высказывания (умозаключения, рассуждения) в виде формулы
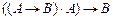 ;
;
3) правило подстановки 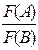 .
.
Фиксируем логико-математический язык первого порядка L. Аксиомами исчисления высказываний(ИВ) в языке Lназываются формулы этого языка, имеющие один из следующих видов:
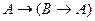 , (1)
, (1)
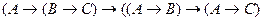 , (2)
, (2)
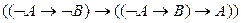 .(3)
.(3)
Здесь A, B, C – произвольные формулы языка L, так что каждая строка приведенного списка задает схему аксиом ИВ.
Формулы в ИВ считаются выводимыми из аксиом. В каждом выводе из тавтологий выводятся тавтологии.
Выражение 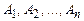 ⊦
⊦ 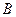 содержит вывод теоремы В из аксиом или гипотез
содержит вывод теоремы В из аксиом или гипотез 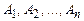 .
.
Формальная система ИВ определяется аксиомами и правилами вывода 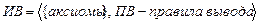 .
.
Выводом назовем любую конечную последовательность формул 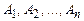 , такую, что каждая формула этой последовательности есть либо аксиома, либо совпадает с какой-либо предыдущей формулой этой последовательности, либо получается из каких-то предыдущих формул этой последовательности с помощью одного из правил вывода. При этом получается вывод последней формулы, и формула
, такую, что каждая формула этой последовательности есть либо аксиома, либо совпадает с какой-либо предыдущей формулой этой последовательности, либо получается из каких-то предыдущих формул этой последовательности с помощью одного из правил вывода. При этом получается вывод последней формулы, и формула 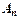 - выводима, или, что то же самое, теорема теории. Будем записывать это в виде Г⊦A (выводимость или секвенция).
- выводима, или, что то же самое, теорема теории. Будем записывать это в виде Г⊦A (выводимость или секвенция).
Список Г может быть пуст, тогда имеет место вывод A без гипотез, формула A выводима в ИВ, записывается это в виде ⊦A.
Пример.
Вывести в теории L теорему (A  A).
A).
Решение.
Возьмем в качестве примера первой формулы вывода аксиому (2). Применим к ней правило подстановки в виде:
( 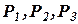
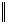 A, (A
A, (A  A), A).
A), A).
Получим
((A  ((A
((A  A)
A)  A))
A))  ((A
((A  (A
(A  A))
A))  (A
(A  A))). (а)
A))). (а)
Из аксиомы (1) подстановкой ( 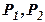
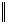 A, (A
A, (A  A)) получим:
A)) получим:
(A  ((A
((A  A)
A)  A)). (б)
A)). (б)
Применим правило (MP) к (а) и (б):
((A  (A
(A  A))
A))  (A
(A  A)). (в)
A)). (в)
Из аксиомы (1) подстановкой ( 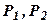
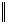 A, A) получим:
A, A) получим:
((A  (A
(A  A))). (г)
A))). (г)
Применяя (МР) к (в) и (г), окончательно получим:
(A  A). (д)
A). (д)
Запишем правила вывода в исчислении высказываний.
Дата добавления: 2016-04-11; просмотров: 2944;
