Логический переход от посылок к заключению называется выводом.
Для логической правильности вывода необходимы следующие отношения:
а) если Р = «истина», то и S должна быть = «истина».
б) если Р = «ложь», то из «лжи» может следовать всё, что угодно, т.е. заключение S может быть и ложным и истинным.
Формула B называется логическим следствием формул A1, A2, …, An, если при любых значениях, входящих в них, элементарных высказываний формула B принимает значение истинно всякий раз, когда формулы A1, A2, …, An принимают значение истинно. Обозначается A1, A2, …, An ├ B.
Из определения логического следования вытекает:
1. Тавтология логически следует из любой формулы.
2. Из противоречия логически следует любая формула.
Теорема 1. Из A логически следует B тогда и только тогда, когда тавтологией является A 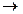 B.
B.
Теорема 2. A1, A2,…, An╞ B тогда и только тогда, когда является тавтологией
A1&A2& …& An 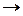 B.
B.
Теорема 3. Из формул A1, A2,…, An , B логически следует C тогда и только тогда, когда из формул A1, A2, …, An логически следует B 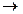 C.
C.
Следствие 1. Из A и B логически следует C тогда и только тогда, когда тавтологией является
A 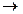 (B
(B 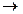 C).
C).
Следствие 2. Из формул A1, A2, …, An логически следует B тогда и только тогда, когда тавтологией является
A1 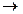 (A2
(A2 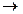 … (An
… (An 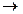 B)…).
B)…).
Дедуктивные умозаключения - те умозаключения, у которых между
посылками и заключениями имеется отношение логического следования.
Правила дедуктивного вывода определяются характером посылок,
которые могут быть простыми (категорическими) или сложными суждениями. В зависимости от количества посылок дедуктивные выводы из категорических суждений делятся на непосредственные, в которых заключение выводится из одной посылки, и опосредованные, в которых заключение выводится из двух посылок.
Непосредственными умозаключениями называются дедуктивные умозаключения, делаемые из одной посылки. К ним в традиционной логике
относятся следующие: превращение, обращение, противопоставление
предикату и умозаключения по логическому квадрату.
Превращение - вид непосредственного умозаключения, при котором
изменяется качество посылки без изменения ее количества, при этом предикат заключения является отрицанием предиката посылки.
По качеству связи категорические суждения делятся на утвердительные
и отрицательные, например: S есть P, S не есть не P.
Обращением называется непосредственное умозаключение, в
котором в заключении (в новом суждении) субъектом является предикат, а
предикатом - субъекта исходного суждения, т. е. происходит перемена мест
субъекта и предиката при сохранении качества суждения. Например: S есть P -> P есть S.
Противопоставление предикату – это непосредственное умозаключение, при котором (в заключении) предикатом является субъект, субъектом - понятие, противоречащее предикату исходного суждения, и связка меняется на противоположную.
Например:
S есть P. -> не-P не есть S.
Иными словами, мы делаем таким образом:
1) вместо P берем не P;
2)меняем местами S и не-P;
3) связку меняем на противоположную.
Например, дано суждение: "Все львы - хищные животные". В результате
противопоставления предикату получим суждение: "Ни одно нехищное животное не является львом".
Противопоставление предикату можно рассматривать как результат двух последовательных непосредственных умозаключений – сначала превращения, затем обращения превращенного суждения.
Простой категорический силлогизм (простое дедуктивное умозаключение) - такое умозаключение, в котором заключение и посылки являются простыми категорическими суждениями.
Категорические суждения - такие, в которых мысль утверждается или отрицается вполне определенно, без всяких условий, и которые имеют субъектно-предикатную структуру. Например: «Все адвокаты - юристы. Петров - адвокат. Петров – юрист».
Проанализируем структуру силлогизма. Понятия, входящие в состав силлогизма, называются терминами силлогизма. Различают меньший, больший и средний термины. Меньший термин - понятие, которое в заключении является субъектом (в нашем примере - понятие «Петров») и обозначается буквой «S». Больший термин - понятие, которое в заключении является предикатом («юрист») и обозначается «Р». Средний термин - понятие, которое входит в обе посылки и не входит в заключение («адвокат»), обозначается буквой «М». Схема силлогизма:«Все М есть Р. S есть М. S есть Р».
Объединенная классификация простых категорических суждений
«А» – общеутвердительные суждения. Их структура «Все S есть Р».
«I» – частноутвердительные суждения - «Некоторые S есть Р».
«Е» – общеотрицательные суждения - «Ни одно S не есть Р».
«О» – частноотрицательные суждения - «Некоторые S не есть Р».
Для иллюстрации отношений между простыми категорическими суждениями используется так называемый логический квадрат. Суждения называются совместимыми по истине, если они оба одновременно могут быть истинными. Отношения совместимости по истине: подчинение (отношения между А и I, Е и О), частичной совместимости (от-ношения между I и О). Суждения называются несовместимыми по истине, если они не могут быть одновременно истинными. Отношения несовместимости по истине: противоположность (между А и Е) и противоречие (между I и Е, и между А и О).
Закономерности по логическому квадрату:
- При отношениях подчинения действует следующая закономерность: если истинно общее (А или Е), то истинно частное (I или О); если ложно частное (I или О), то ложно общее (А или Е).
- При частичной совместимости: оба суждения могут быть одновременно истинными, но не могут быть одновременно ложными, поэтому: если одно ложное, то другое обязательно истинное.
- При отношениях противоположности действует следующая закономерность: оба суждения могут быть одновременно ложными, но не могут быть одновременно истинными. Поэтому, если одно из них истинное, то другое - обязательно ложное. При противоречии оба суждения не могут быть одновременно ни истинными, ни ложными. Значит, если одно из них истинное, то другое обязательно ложное, и наоборот.
Пример. Определите тип суждения «Некоторые студенты нашей группы пошли в кино» (А, Е, I, О). Сформулируйте стандартную форму данного суждения и остальных суждений с теми же субъектом и предикатом. Считая данное суждение истинным, определите истинность, ложность или неопределенность остальных суждений с теми же субъектом и предикатом по логическому квадрату.
Решение:
Суждение «Некоторые студенты нашей группы пошли в кино» - частноутвердительное ( I );
А: «Все студенты нашей группы пошли в кино» - неопределенное;
Е: «Ни один студент нашей группы не пошел в кино» - ложь.
О: «Некоторые студенты нашей группы не пошли в кино» - неопределенное.
Пример. Произведите отрицание суждения «Некоторые студенты нашей группы пошли в кино» таким образом, чтобы результат отрицания не содержал внешних знаков отрицания (с помощью логического квадрата).
Решение: Для суждения типа I противоречащим является суждение типа Е: «Ни один студент нашей группы не пошел в кино».
Дата добавления: 2016-04-11; просмотров: 1389;
