Индивидуальное задание. 1. Дана машина Тьюринга с ленточным алфавитом А = ( ,1), алфавитом внутренних состояний Q и со следующей функциональной схемой (программой):

1. Дана машина Тьюринга с ленточным алфавитом А = ( ,1), алфавитом внутренних состояний Q и со следующей функциональной схемой (программой):

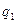
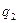
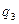
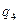
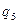
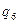
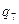
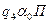
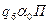
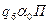
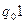
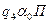
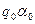
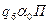
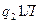
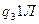
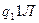
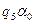
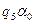
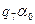
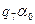
определите, в какое слово перерабатывает машина данное входное слово, исходя из состояний:

а) начального стандартного положения;

b) обозревается крайняя правая ячейка, начальное состояние .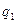

1.11111111 1;

1.211111 11;

1.31 11 111;

1.41 11111 1;

1.51111111 1;

1.6111 11 111;

1.711 111111;

1.8111111 1 1;

1.91 1111 111;

1.1011 11111 1;

1.11111111 11;

1.1211 11111 1;

1.1311 1111 11;

1.141 1111 111;

1.15 1 1111111.

2По словесному описанию машины Тьюринга построить ее программу на указанном ленточном алфавите.

2.1 Начав работу с первой единицы массива из единиц, машина сдвигает его на две ячейки вправо, не изменяя остального содержимого ленты, и останавливается на последней единице перенесенного массива, алфавит ( ,1).

2.2 Начав двигаться влево от произвольной ячейки, головка находит первую при таком перемещении ячейку с единицей (если такая встретится на пути) и, сделав один шаг вправо, останавливается на соседней ячейке. Содержимое ленты не меняется.

2.3 Машина начинает работу с самой левой непустой ячейки и отыскивает нуль, примыкающий с левой стороны к первому справа массиву из трех единиц, окаймленному нулями. Головка останавливается на первой единице найденного массива (если такой есть). Содержимое ленты не меняется.

2.4 Головка машины, начав работу с произвольной ячейки, содержащей единицу, двигается влево до тех пор, пока не пройдет подряд пять нулей. Головка останавливается на первой ячейке слева за этими пятью нулями, напечатав в ней единицу. Остальное содержимое ленты не меняется.

2.5 При заданном n ≥1 головка машины, начав работу с произвольной ячейки и двигаясь вправо, записывает подряд 2n нулей и останавливается на последнем из них.

2.6 Головка машины, двигаясь вправо от какой-либо пустой ячейки, находит первый при таком перемещении массив, содержащий не менее семи единиц, стирает в нем первые семь единиц и останавливается на самой правой из ячеек, в которых были стерты единицы. Остальное содержимое ленты не меняется.

2.7 При заданном значении n головка машины из n записанных единиц оставляет на ленте n − 2 единицы, так же записанных подряд, если n ≥ 2 , и работает вечно, если n = 0 или n = 1.

2.8 Начав работу с последней единицы массива из единиц, машина сдвигает его на две ячейки влево, не изменяя остального содержимого ленты, и останавливается на последней единице перенесенного массива.

2.9 На ленту подряд вписаны два конечных набора единиц, разделенные звездочкой. Составьте программу машины Тьюринга, которая выписывала бы подряд (без разделения звездочкой) столько единиц, сколько их в обоих наборах (сложение единиц).

2.10 Дана строка из букв а и b. Разработайте машину Тьюринга, которая переместит все буквы а в левую, а буквы b в правую часть строки. Каретка находится над крайним левым символом строки.

2.11 На ленте машины Тьюринга записано число в десятичной системе счисления. Каретка находится над крайней правой цифрой. Запишите цифры этого числа в обратном порядке.

2.12 На информационной ленте машины Тьюринга находится массив, состоящий только из символов А и B. Сожмите массив, удалив из него все элементы B.

2.13 Составьте программу машины Тьюринга, которая складывала бы числа: 1 + 2.

2.14 Составьте программу машины Тьюринга, которая вычитала бы числа: 2-1.

2.15 Составьте программу машины Тьюринга, которая складывала бы числа: 2 + 2.