Индивидуальное задание
3Запишите простой категорический силлогизм в виде формулы логики предикатов. Проверьте правильность рассуждения с помощью кругов Эйлера-Венна, методом резолюций.
3.1 Некоторые нелюбезные замечания вызывают раздражение. Ни одно критическое замечание не любезно. Значит, все критические замечания вызывают раздражение.
3.2 Я – человек. Ты – не я. Значит, ты – не человек.
3.3 Жизнь – борьба. Дзюдо – борьба. Значит, жизнь – дзюдо.
3.4 Все педагоги воспитанны. Он не педагог. Значит, он не воспитан.
3.5 Экспрессы здесь никогда не останавливаются. Ни один поезд сегодня здесь не остановился. Значит, все поезда, проходившие сегодня - экспрессы.
3.6 Большинство учителей имеет высшее образование. Иванов – учитель. Значит, Иванов имеет высшее образование.
3.7Ни один ведущий редактор не подпишет непрочитанную рукопись. Иванов не является ведущим редактором. Значит, он подпишет непрочитанную рукопись.
3.8Во всех городах за полярным кругом бывают белые ночи. Санкт-Петербург не находится за полярным кругом. Значит, в Санкт-Петербурге нет белых ночей.
3.9Большая часть студентов нашей группы изучает английский язык. Петров – студент нашей группы. Значит, он изучает английский.
3.10 Все студенты нашей группы успешно сдали экзамены. Петров успешно сдал экзамен. Значит, он студент нашей группы.
3.11 Математическая логика изучает формы и законы правильного мышления. Учение о понятии есть часть математической логики. Следовательно, оно изучает законы и формы правильного мышления.
3.12Мысль - это движение. Движение есть свойство всей материи. Значит, мысль есть свойство всей материи.
3.13 Все школьники сдают экзамены. Васильев не является школьником. Следовательно, Васильев не сдает экзамены.
3.14 Закон противоречия – закон мышления. Закон противоречия сформулирован Аристотелем. Значит, некоторые законы мышления сформулировал Аристотель.
3.15 Некоторые студенты – спортсмены. Иванов – студент. Значит, он – спортсмен.
4В приведенных силлогизмах установите следствие, большую и меньшую посылки, проверьте достоверность вывода.
4.1 Каждый совершивший преступление должен быть подвергнут справедливому наказанию. Обвиняемый совершил преступление, следовательно, он должен быть подвергнут справедливому наказанию.
4.2 Ни один невиновный не должен быть привлечен к уголовной ответственности. Значит, Н. не должен быть привлечен к уголовной ответственности, так как он невиновен.
4.3Некоторые деятели искусства – талантливые люди. Значит, некоторые писатели талантливы, ибо все писатели – деятели искусства.
4.4 Некоторые металлы не тонут в воде, так как натрий металл, а натрий не тонет в воде.
4.5 Иванов не является сильным шахматистом, поэтому он не знает теорию шахматной игры, а все сильные шахматисты знают теорию шахматной игры.
4.6 Некоторые рыбы не мечут икру, так как голомянка не мечет икру, а голомянка – рыба.
4.7Все студенты 1 курса изучают иностранные языки, значит, Петров – студент первого курса, так как он изучает иностранные языки.
4.8 Ни одна книга не является ненужной. Некоторые учебники – книги. Значит, все учебники нужны.
4.9 Ни один человек не лишен способностей. Некоторые люди – студенты. Значит, некоторые, лишенные способностей, не студенты.
4.10 Существуют равнобедренные треугольники. Не все треугольники равносторонние. Значит, некоторые равнобедренные треугольники - равносторонние.
4.11 Некоторые параллелограммы - ромбы, все ромбы – четырехугольники, значит некоторые четырехугольники – не ромбы.
4.12 Все круглые предметы не имеют углов, значит все треугольные предметы не могут быть круглыми;
4.13Не все треугольники - равносторонние. Значит, какие-то равнобедренные треугольники – не равносторонние.
4.14Имеются положительные числа. Ни одно отрицательное число не является натуральным. Значит, некоторые натуральные числа положительные.
4.15Все зайцы не хищники, некоторые хищники - волки, значит, все волки - не зайцы.
Теория алгоритмов
Машина Тьюринга
Машина Тьюринга является расширением модели конечного автомата, расширением, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу.
Машина Тьюринга представляет собой автомат, с конечным числом состояний, соединенный с внешней памятью – лентой, разбитой на ячейки, в каждой из которых записан один из символов конечного алфавита А= { a1, ... am}.
Автомат связан с лентой с помощью головки, которая в каждый момент времени обозревает одну ячейку ленты, и в зависимости от символа в этой ячейке и состояния управляющего устройства записывает в ячейку символ (совпадающий с прежним или пустой), сдвигается на ячейку вправо или влево или остается на месте. Среди состояний управляющего устройства выделим начальное состояние 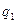 и заключительное состояние
и заключительное состояние 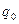 . В начальном состоянии машина находится перед началом работы. Попав в заключительное состояние, машина останавливается. Т. о. память машины Т – это конечное множество состояний (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, однако в любой момент времени лишь конечный отрезок ленты будет заполнен символами. Поэтому важна не фактическая бесконечность ленты, а ее неограниченность, т.е. возможность писать на ней сколь угодно длинные, но конечные слова.
. В начальном состоянии машина находится перед началом работы. Попав в заключительное состояние, машина останавливается. Т. о. память машины Т – это конечное множество состояний (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, однако в любой момент времени лишь конечный отрезок ленты будет заполнен символами. Поэтому важна не фактическая бесконечность ленты, а ее неограниченность, т.е. возможность писать на ней сколь угодно длинные, но конечные слова.
Данные в машине Т – это слова в алфавите ленты; на ленте записываются и исходные данные и окончательные результаты. Элементарные шаги – это считывание и запись символов, сдвиг головки на ячейку влево или вправо, а также переход управляющего устройства в следующее состояние.
Детерминированность машины Т определяется следующим образом: для любого внутреннего состояния qiи символа aj однозначно заданы:
а) следующее состояние qi`;
б) символ aj`, который надо записать в ту же ячейку вместо aj(стирание – это запись пустого символа );
в) направление сдвига головки dk(L – влево, R – вправо, E – на месте).
Это задание может описываться:
− системой правил:
qiaj qi`aj`dk;
− таблицей, строкам которой соответствуют состояния, столбцам – входные символы, а на пересечении записана тройка символов:
− qi`aj`dk;
− блок-схемой (диаграммой переходов), в которой состояниям соответствуют вершины, а правилу вида: qiaj qi`aj`dk– ребро, ведущее из qi в qi`.
Полное состояние машины Т, по которому однозначно можно определить ее дальнейшее поведение, определяется ее внутренним состоянием, состоянием ленты (т.е. символом, записанным на ленте) и положением головки на ленте.
Полное состояние будем называть конфигурацией или машинным словом. Стандартной начальной конфигурацией называется конфигурация вида q1 , то есть конфигурацию, содержащую начальное состояние, в котором головка обозревает крайний левый символ слова, написанного на ленте. Аналогично, стандартной заключительной конфигурацией называется конфигурация вида 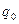 . Ко всякой незаключительной конфигурации К машины Т применима ровно одна команда вида:
. Ко всякой незаключительной конфигурации К машины Т применима ровно одна команда вида:
qiaj qi`aj`dk,
которая конфигурацию К переводит в конфигурацию К. Последовательность вида: К1 К2 К3 ... однозначно определяется исходной конфигурацией К1и полностью описывает работу машины Т, начиная с К1.
На примере машины Тьюринга хорошо прослеживаются свойства алгоритмов, так как машина Тьюринга обладает всеми свойствами алгоритма:
1) дискретность − машина Тьюринга может перейти к (к + 1) - му шагу только после выполнения каждого шага, т.к именно каждый шаг определяет, каким будет (к + 1) - й шаг;
2) понятность − на каждом шаге в ячейку пишется символ из алфавита, автомат делает одно движение (Л, П, Н), и машина Тьюринга переходит в одно из описанных состояний;
3) детерминированность − в каждой клетке таблицы машины Тьюринга записан лишь один вариант действия, на каждом шаге результат определен однозначно, следовательно, последовательность шагов решения задачи определена однозначно, т. е. если машине Тьюринга на вход подают одно и то же входное слово, то выходное слово каждый раз будет одним и тем же;
4) результативность − содержательно результаты каждого шага и всей последовательности шагов определены однозначно, следовательно, правильно написанная машина Тьюринга за конечное число шагов перейдет в состояние q0, т.е. за конечное число шагов будет получен ответ на вопрос задачи;
5) массовость − каждая машина Тьюринга определена над всеми допустимыми словами из алфавита, в этом и состоит свойство массовости. Каждая машина Тьюринга предназначена для решения одного класса задач, т.е. для каждой задачи пишется своя (новая) машина Тьюринга.
Если для словарной функции f (применимой к словам, заданным на входном алфавите машины Тьюринга) существует машина Т, которая ее правильно вычисляет, f называется правильно вычислимой по Тьюрингу. С другой стороны, любой правильно вычисляющей машине Т можно поставить в соответствие вычисляемую ею функцию.
Основной теоремой теории алгоритмов является тезис Тьюринга: «Всякий алгоритм может быть реализован машиной Тьюринга». Доказать тезис нельзя, поскольку само понятие алгоритма является неточным. Подтверждением тезиса являются во-первых, математическая практика, а во-вторых, то, что описание алгоритма в терминах любой другой известной алгоритмической модели может быть сведено к его описанию в виде машины Тьюринга.
В силу тезиса Тьюринга эту задачу можно сформулировать как задачу о построении машины Тьюринга. Эта задача называется проблемой остановки, в связи с чем доказана теорема: «Не существует машины Тьюринга, решающей проблему остановки для произвольной машины Тьюринга».
Рассмотрим примеры применения машины Тьюринга к словам.
Пример. Найти результат применения машины Тьюринга, заданной следующими командами: 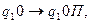
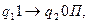
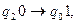
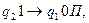 к записям на ленте:
к записям на ленте: 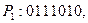
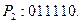
Решение:
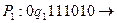
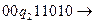
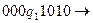
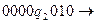
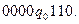
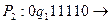
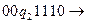
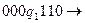
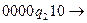
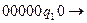
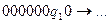
Пример. Построить машину Тьюринга, правильно вычисляющую функцию 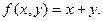
Решение:
В начальном состоянии на ленте будет записан входное слово вида: 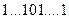 , где первые
, где первые 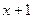 единиц представляют собой число
единиц представляют собой число 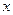 , вторые
, вторые 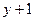 единиц – число
единиц – число 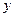 , 0 является разделителем между числами. Необходимо сконструировать машину Тьюринга (записать команды), в результате работы которой на ленте будет записано
, 0 является разделителем между числами. Необходимо сконструировать машину Тьюринга (записать команды), в результате работы которой на ленте будет записано 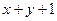 единиц.
единиц.
Команды 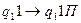 ,
, 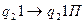 передвигают положение управляющей головки (обозреваемой ячейки) на одну позицию вправо, команда
передвигают положение управляющей головки (обозреваемой ячейки) на одну позицию вправо, команда 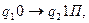 заменяет ноль на единицу и также передвигает положение УГ вправо на 1 позицию. Применение таких команд из начального стандартного положения (обозревается крайняя левая ячейка, МТ находится в начальном состоянии
заменяет ноль на единицу и также передвигает положение УГ вправо на 1 позицию. Применение таких команд из начального стандартного положения (обозревается крайняя левая ячейка, МТ находится в начальном состоянии 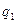 ) позволяет переместить положение УГ на крайнюю правую единицу, причем разделяющий ноль будет заменен на 1, таким образом на ленте будет записано
) позволяет переместить положение УГ на крайнюю правую единицу, причем разделяющий ноль будет заменен на 1, таким образом на ленте будет записано 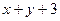 единицы, две лишние единицы надо заменить нулями, затем можно переместить положение УГ влево до крайней левой ячейки и остановиться.
единицы, две лишние единицы надо заменить нулями, затем можно переместить положение УГ влево до крайней левой ячейки и остановиться.
Следующие команды: 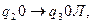
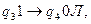
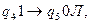 стирают две единицы и перемежают положение УГ влево, команда
стирают две единицы и перемежают положение УГ влево, команда 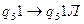 позволяет переместить положение УГ к крайней левой ячейке, не стирая единиц, команда
позволяет переместить положение УГ к крайней левой ячейке, не стирая единиц, команда 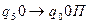 позволяет остановить работу Машины Тьюринга.
позволяет остановить работу Машины Тьюринга.
Упражнения
1. Найти результат применения машины Тьюринга к слову на ленте Х=0111110:
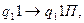
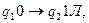
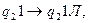
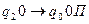 .
.
2. Найти результат применения машины Тьюринга к слову на ленте Х=011010:
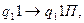
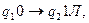
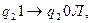
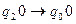 .
.
3. Построить машину Тьюринга, вычисляющую функцию 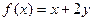 .
.
4. Построить машину Тьюринга, реализующую функцию 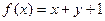 .
.
5.Реализовать машину Тьюринга, приписывающую к слову P=aabbbc справа символ b.
Дата добавления: 2016-04-11; просмотров: 1874;
