Рекурсивные функции
Оператором примитивной рекурсии R называются подстановки, удовлетворяющие системе уравнений: 
f(x1,...,xn)= g(x1,...,xn),
f(x1,...,xn,y+1)= h(x1,...,xn,y,f(x1,...,xn,y)),
которая называется схемой примитивной рекурсии.
Функция называется примитивно-рекурсивной, если она может быть получена из константы 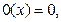 функции следования
функции следования 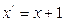 и функций тождества
и функций тождества 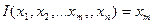 с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.
с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.
Примерами примитивно-рекурсивных функций являются:
1. 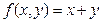 ;
;
2. 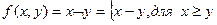 ; 0 в противном случае;
; 0 в противном случае;
3.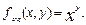
Ограниченный оператор минимизации – применяется к предикатам:
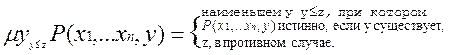
Из предиката 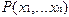 с помощью оператора минимизации получается функция
с помощью оператора минимизации получается функция 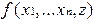 . Ограничение z в операторе дает гарантию окончания вычислений, поскольку оно оценивает сверху число вычислений предиката
. Ограничение z в операторе дает гарантию окончания вычислений, поскольку оно оценивает сверху число вычислений предиката 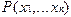 .
.
Еще один ПР-оператор – оператор одновременной рекурсии 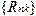 . C его помощью строится рекурсивное описание сразу нескольких функций
. C его помощью строится рекурсивное описание сразу нескольких функций 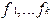 от (n-1)-ой переменной, причем значение каждой функции в точке y+1 зависит от значения всех функций в точке y:
от (n-1)-ой переменной, причем значение каждой функции в точке y+1 зависит от значения всех функций в точке y:
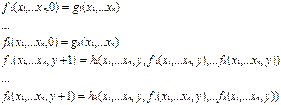
Из простейших функций - константы 0, функции следования и функций тождества с помощью операторов суперпозиции и примитивной рекурсии может быть получено огромное разнообразие функций, включающих основные функции арифметики, алгебры и анализа (с поправкой на целочисленность).
Рекурсивные функции подразделяются на группы: примитивно-рекурсивные, частично-рекурсивные и общерекурсивные. Примитивно-рекурсивные функции могут быть получены с помошью операторов примитивной рекурсии и минимизации.
Функция называется частично-рекурсивной, если она может быть построена из простейших функций: константы 0, тождества и следования, с помощью конечного числа применений операторов примитивной рекурсии и минимизации.
По определению -оператор применяется к предикатам. Поскольку в теории рекурсивных функций истинность предиката всегда связана со справедливостью некоторого равенства, то -оператору можно придать стандартную форму:
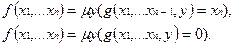
Если на данном наборе уравнение 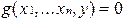 не имеет решения, функция считается неопределенной, среди рекурсивных функций появляются не полностью определенные, т. е. частичные функции. Частично-рекурсивная функция называется общерекурсивной, если она всюду определена.
не имеет решения, функция считается неопределенной, среди рекурсивных функций появляются не полностью определенные, т. е. частичные функции. Частично-рекурсивная функция называется общерекурсивной, если она всюду определена.
Пример. Найти функцию, получаемую из 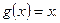
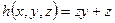 с помощью операций примитивной рекурсии.
с помощью операций примитивной рекурсии.
Решение:
Запишем операторы примитивной рекурсии для функции двух переменных 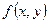 :
:
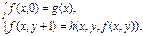
Из рекурсивных соотношений получим значения функции 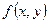 на каждом шаге (при
на каждом шаге (при 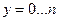 ), где у – номер шага.
), где у – номер шага.
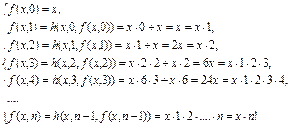
Итак, выражение для рекурсивной функции - 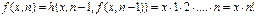 .
.
Пример. Найти функции, получаемые из данной функции 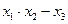 с помощью минимизации по каждой переменной.
с помощью минимизации по каждой переменной.
Решение:
Минимизируем функцию по переменной 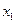 , решим уравнение:
, решим уравнение:
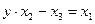 .
.
При 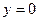 получим
получим 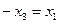 , что возможно для неотрицательных чисел только при
, что возможно для неотрицательных чисел только при 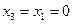 , тогда оператор минимизации по первой переменной определен следующим образом:
, тогда оператор минимизации по первой переменной определен следующим образом:

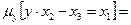 0 при
0 при 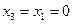 ,
,
не определен в остальных случаях.
Минимизируем функцию по переменной 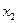 , решим уравнение:
, решим уравнение:
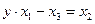 .
.
При 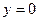 получим
получим 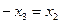 , что возможно для неотрицательных чисел только при
, что возможно для неотрицательных чисел только при 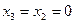 , тогда оператор минимизации по первой переменной определен следующим образом:
, тогда оператор минимизации по первой переменной определен следующим образом:

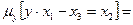 0 при
0 при 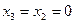 ,
,
не определен в остальных случаях.
Минимизируем функцию по переменной 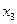 , решим уравнение:
, решим уравнение:
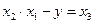 .
.
При 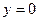 получим
получим 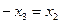 , что возможно для неотрицательных чисел только при
, что возможно для неотрицательных чисел только при 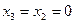 , тогда оператор минимизации по первой переменной определен следующим образом:
, тогда оператор минимизации по первой переменной определен следующим образом:

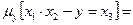
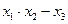 при
при 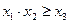 ,
,
не определен в остальных случаях.
Тезис Черча: всякая функция, вычислимая некоторым алгоритмом, частично-рекурсивна. Это утверждение – аналог тезиса Тьюринга: всякий алгоритм может быть реализован машиной Тьюринга, для рекурсивных функций. Из сопоставления этих двух тезисов вытекает следующее утверждение (тезис Черча-Тьюринга): функция вычислима машиной Тьюринга тогда и только тогда, когда она частично-рекурсивна.
Итак, всякий алгоритм, описанный в терминах частично-рекурсивных функций можно реализовать машиной Тьюринга и наоборот.
Множество всех алгоритмов счетно, что означает наличие взаимно-однозначного соответствия между алгоритмами и числами натурального ряда, т.е. функции типа:
: Al N.
Такая функция называется нумерацией алгоритмов, а ее значение (А) – номером алгоритма А при нумерации . Из взаимной однозначности отображения следует, что существует обратная функция -1(n)=Аn, восстанавливающая по номеру n описание алгоритма Аn. Существование нумераций позволяет работать с алгоритмами как с числами.
Все примитивно-рекурсивные функции могут быть реализованы на машине тьюринга
Пример. Реализуем функцию константу 0:
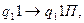
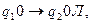
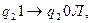
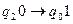 .
.
Упражнения
1. Составить программу МТ для следующих функций: 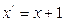 ;
; 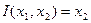 ;
; 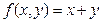 ;
; 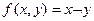 ;
; 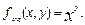
2.Найти функцию 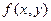 , получаемую из
, получаемую из 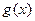 ,
, 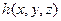 с помощью операции примитивной рекурсии:
с помощью операции примитивной рекурсии: 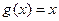 ,
, 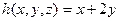 .
.
Дата добавления: 2016-04-11; просмотров: 3209;
