Нормальные алгоритмы Маркова
Алфавитом будем называть любое непустое множество. Его элементы называются буквами, а любые последовательности букв - словами в данном алфавите. Для удобства рассуждений допускаются пустые слова (они не имеют в своем составе ни одной буквы). Пустое слово (пустой символ) обозначается как 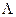 . Если А и В — два алфавита, причем А
. Если А и В — два алфавита, причем А 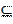 В, то алфавит В называется расширением алфавита А.
В, то алфавит В называется расширением алфавита А.
Слова алфавита (набор символов) обозначаются буквами: Р, Q, R... Одно слово может быть составной частью другого слова, тогда первое называется подсловом второго или вхождением во второе.
Марковской подстановкой называется операция над словами, задаваемая с помощью упорядоченной пары слов (Р, Q), состоящая в следующем:
1) В заданном слове R находят первое вхождение слова Р (если таковое имеется);
2) Не изменяя остальных частей слова R, заменяют в нем это вхождение словом Q. Полученное слово называется результатом применения марковской подстановки (Р, Q) к слову R. Если же первого вхождения Р в слово R нет (и, следовательно, вообще нет ни одного вхождения Р в R), то считается, что марковская подстановка (Р, Q) неприменима к слову R.
Пример. Примеры марковских подстановок рассмотрены в таблице, в каждой строке которой сначала дается преобразуемое слово, затем применяемая к нему марковская подстановка и, наконец, получающееся в результате слово:
| Преобразуемое слово | Марковская подстановка | Результат |
| 138 578 926 | (8 578 9, 00) | 130 026 |
| тарарам | (ара, 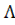 ) )
| трам |
| шрам | (ра, ар) | шарм |
| функция | ( 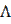 , , 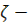 ) )
| 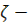 функция функция
|
| логика | (ика, 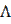 ) )
| лог |
| книга | ( 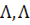 ) )
| книга |
| поляна | (пор, т) | [неприменима] |
Для обозначения марковской подстановки (Р, Q) используется запись 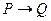 . Она называется формулой подстановки (Р, Q). Подстановки вида
. Она называется формулой подстановки (Р, Q). Подстановки вида 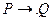 будем называть заключительными. Для обозначения таких подстановок будем использовать запись
будем называть заключительными. Для обозначения таких подстановок будем использовать запись 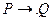 , называя ее формулой заключительной подстановки. Слово Р называется левой частью, a Q -правой частью в формуле подстановки.
, называя ее формулой заключительной подстановки. Слово Р называется левой частью, a Q -правой частью в формуле подстановки.
Упорядоченный конечный список формул подстановок:
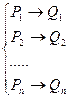
в алфавите А называется схемой (или записью) нормального алгоритма в А.
Нормальным алгоритмом Маркова в алфавите А называется следующее правило построения последовательности Vi слов в алфавите А, исходя из данного слова V в этом алфавите. В качестве начального слова V0 последовательности берется слово V. Пусть для некоторого 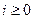 слово Vi построено и процесс построения рассматриваемой последовательности еще не завершился. Если при этом в схеме нормального алгоритма нет формул, левые части которых входили бы в Vi то Vi+1 полагают равным Vi, и процесс построения последовательности считается завершившимся. Если же в схеме имеются формулы с левыми частями, входящими в Vi, то в качестве Vi+l берется результат марковской подстановки правой части первой из таких формул вместо первого вхождения ее левой части в слово Vi. Процесс построения последовательности считается завершившимся, если на данном шаге была применена формула заключительной подстановки, и продолжающимся- в противном случае. Если процесс построения упомянутой последовательности обрывается, то говорят, что рассматриваемый нормальный алгоритм применим к слову V. Последний член W последовательности называется результатом применения нормального алгоритма к слову V. Говорят, что нормальный алгоритм перерабатывает V в W.
слово Vi построено и процесс построения рассматриваемой последовательности еще не завершился. Если при этом в схеме нормального алгоритма нет формул, левые части которых входили бы в Vi то Vi+1 полагают равным Vi, и процесс построения последовательности считается завершившимся. Если же в схеме имеются формулы с левыми частями, входящими в Vi, то в качестве Vi+l берется результат марковской подстановки правой части первой из таких формул вместо первого вхождения ее левой части в слово Vi. Процесс построения последовательности считается завершившимся, если на данном шаге была применена формула заключительной подстановки, и продолжающимся- в противном случае. Если процесс построения упомянутой последовательности обрывается, то говорят, что рассматриваемый нормальный алгоритм применим к слову V. Последний член W последовательности называется результатом применения нормального алгоритма к слову V. Говорят, что нормальный алгоритм перерабатывает V в W.
Последовательность Vi, будем записывать следующим образом: 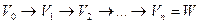 .
.
Если алгоритм Маркова задан в некотором расширении алфавита А, то он называется - нормальный алгоритм над алфавитом А.
Рассмотрим примеры нормальных алгоритмов.
Пример. Пусть А = {a,b} — алфавит. Рассмотрим следующую схему нормального алгоритма в А:
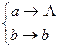
Рассмотрим последовательность слов: aabab → abab. Всякое слово V в алфавите А, содержащее хотя бы одно вхождение буквы а, он перерабатывает в слово, получающееся из V вычеркиванием в нем самого левого (первого) вхождения буквы а. Пустое слово он перерабатывает в пустое. Алгоритм не применим к таким словам, которые содержат только букву b.
Пример. Пусть А = {a,b} — алфавит. Рассмотрим следующую схему нормального алгоритма в А:
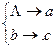
Рассмотрим последовательность слов: bab → 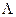 abab → aabab → aacab. Первая подстановка применима всегда, т. к. пустой символ мы можем приписать слева от любого слова.
abab → aabab → aacab. Первая подстановка применима всегда, т. к. пустой символ мы можем приписать слева от любого слова.
Пример. Пусть A = {a0, a1 ..., an} — алфавит. Рассмотрим схему:
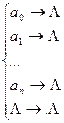
Она определяет нормальный алгоритм, перерабатывающий всякое слово (в алфавите А) в пустое слово: 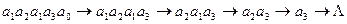 .
.
Как и машины Тьюринга, нормальные алгоритмы не производят вычислений, а производят преобразования слов, заменяя в них одни буквы другими по предписанным им правилам, результаты применения которых можно интерпретировать как вычисления.
Пример. В алфавите А = {1} схема 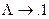 определяет нормальный алгоритм, который к каждому слову в алфавите А = {1}, вида:
определяет нормальный алгоритм, который к каждому слову в алфавите А = {1}, вида: 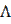 , 1, 11, 111, 1111, 11111 и т. д., приписывает слева 1. Следовательно, алгоритм реализует (вычисляет) функцию
, 1, 11, 111, 1111, 11111 и т. д., приписывает слева 1. Следовательно, алгоритм реализует (вычисляет) функцию 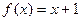 .
.
Пример. Пусть A = {a, b, с, d} — алфавит. Рассмотрим схему:
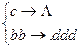
Данная схема удаляет из слова все вхождения символа c, после чего заменяется bb на ddd, затем алгоритм остановится: сbaсbb → babb → baddd.
Задание

Дата добавления: 2016-04-11; просмотров: 2426;
