Правило сложного заключения
Если формулы 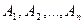 и
и 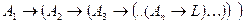 доказуемы, то и формула L доказуема:
доказуемы, то и формула L доказуема:
├А1, ├А2, …,├Аn, ├A1→(A2→(A3→(...(An→L) …)))
├ L
Правило силлогизма
Если доказуемы формулы А→В и В→С, то доказуема формула А→С , т. е.
├А→В,├В→С
├А→С
Правило контр позиции
Если доказуема формула А→В, то доказуема формула 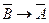 , т. е.
, т. е.
├ А →В
├ 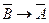
Правило снятия двойного отрицания
Если доказуема формула 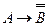 , то доказуема формула
, то доказуема формула 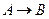 .
.
Если доказуема формула 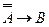 , то доказуема формула
, то доказуема формула 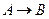 :
:
├ А → 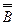
├ 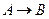 ,
,
├ 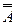 →В
→В
├ 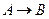 .
.
Теорема о дедукции
Если
j1, j2, …, jn, j ├ ψ,
то
j1, j2, …, jn├ (j → ψ).
Если нужно в некоторой ситуации установить, что 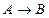 , то допустим (введем гипотезу), что A верно, и докажем B, исходя из этой гипотезы.
, то допустим (введем гипотезу), что A верно, и докажем B, исходя из этой гипотезы.
Применяя к утверждению теоремы снова несколько раз теорему дедукции, можно, очевидно, получить новые следствия:
j1, j2, …, jn−1├ (jn → (j → ψ));
…
├ (j1 → … → (jn−1 → (jn → (j → ψ)))…).
Теорема, обратная к теореме о дедукции
Если
j1, j2, …, jn├ (j → ψ),
то
j1, j2, …, jn, j ├ ψ.,
то есть можно переносить левую часть формулы (посылку) за знак выводимости. Данное действие можно выполнять несколько раз (столько, сколько знаком следствия используется в формуле.
Теорема о полноте
Для того чтобы проверить выводимость формулы в ИВ (исчислении высказываний) достаточно проверить, будет ли формула являться тавтологией ЛВ (логики высказываний).
Следовательно, для того чтобы проверить выводимость формулы - заключения 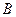 из посылок (гипотез или аксиом)
из посылок (гипотез или аксиом) 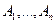 , достаточно проверить, будет ли являться тавтологией формула
, достаточно проверить, будет ли являться тавтологией формула 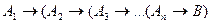 .
.
Упражнения
Построить вывод или обосновать выводимость формулы логики высказываний. Сделать проверку с помощью теоремы о полноте.
1. 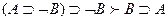 ;
;
2. 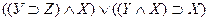 ;
;
3. 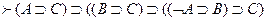 .
.
Дата добавления: 2016-04-11; просмотров: 2078;
