Вибір оптимального рішення за правилом максИмакс
| Варіант рішення | Варіант стану середовища | maxj{V(Ai, Sj)} | maxi mахj{V(Ai, Sj)} | ||
| S1 | S2 | S3 | |||
| А1 | 2,5 | 3,5 | 4,0 | 4,0 | |
| А2 | 1,5 | 2,0 | 3,5 | 3,5 | |
| А3 | 3,0 | 8,0 | 2,5 | 8,0 | А3* |
| А4 | 7,5 | 1,5 | 3,5 | 7,5 |
Мінімакс орієнтований на мінімізацію жалю з приводу втраченого прибутку й допускає розумний ризик заради отримання додаткового прибутку.
Розрахунок критерію складається з чотирьох етапів:
1. Знаходимо кращий результат кожної графи (максимум aij).
2. Визначаємо відхилення від кращого результату кожної окремої графи, тобто maxi aij – aij. Отримані результати створять матрицю ризику (жалю), тому що її елементи — це недоотриманий прибуток від невдало прийнятих рішень, допущених через помилкову оцінку можливої реакції ринку.
3. Для кожного рядка матриці жалю знаходимо максимальне значення.
4. Обираємо рішення, за якого максимальний жаль буде меншим, ніж за інших рішень.
Критерій використовується тоді, коли необхідно обрати стратегію захисту об’єкта від занадто великих утрат. Використання критерію Севіджа є доцільним тільки за умови достатньої фінансової стабільності підприємства, коли є впевненість, що випадковий збиток не призведе до повного краху
Для того щоб застосувати критерій Севіджа, потрібно побудувати матрицю ризику як лінійне перетворення функціоналу оцінювання.
Для побудови матриці ризику використаємо такі формули:
для 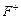
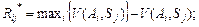 (8)
(8)
для 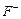
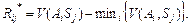 (9)
(9)
Матрицю ризику побудуємо в табл. 6.
Таблиця 6
Побудова матриці ризику
| Варіант рішення | Матриця прибутків (V(Ai, Sj)) | Матриця ризику (Rij) | ||||
| Варіанти станів середовища | Варіанти станів середовища | |||||
| S1 | S2 | S3 | S1 | S2 | S3 | |
| А1 | 2,5 | 3,5 | 4,0 | 7,5 – 2,5 = 5,0 | 8,0 – 3,5 = 4,5 | 4,0 – 4,0 = 0 |
| А2 | 1,5 | 2,0 | 3,5 | 7,5 – 1,5 = 6,0 | 8,0 – 2,0 = 6,0 | 4,0 – 3,5 = 0,5 |
| А3 | 3,0 | 8,0 | 2,5 | 7,5 – 3,0 = 4,5 | 8,0 – 8,0 = 0 | 4,0 – 2,5 = 1,5 |
| А4 | 7,5 | 1,5 | 3,5 | 7,5 – 7,5 = 0 | 8,0 – 1,5 = 6,5 | 4,0 – 3,5 = 0,5 |
Тепер можна застосуватикритерій Севіджадо матриці ризику за формулою:
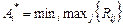 . (10)
. (10)
Таблиця 7
Вибір оптимального рішення за критерієм Севіджа
| Варіант рішення | Варіант стану середовища | maxj{Rij} | mini maxj{Rij} | ||
| S1 | S2 | S3 | |||
| А1 | 5,0 | 4,5 | 5,0 | ||
| А2 | 6,0 | 6,0 | 0,5 | 6,0 | |
| А3 | 4,5 | 1,5 | 4,5 | А3 | |
| А4 | 6,5 | 0,5 | 6,5 |
За критерієм Севіджа оптимальним буде альтернативне рішення А3 (табл. 7).
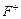
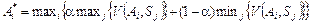 . (5.11)
для
. (5.11)
для 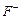
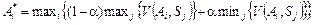 . (5.12)
Оптимальним рішенням за критерієм Гурвіца буде альтернативне рішення А3 (табл. 8).
Таблиця 8
Вибір оптимального рішення за критерієм Гурвіца
. (5.12)
Оптимальним рішенням за критерієм Гурвіца буде альтернативне рішення А3 (табл. 8).
Таблиця 8
Вибір оптимального рішення за критерієм Гурвіца
| Варіант рішення | Варіант стану середовища | maxj {V(Ai, Sj)} | minj {V(Ai, Sj)} | a · maxj{V(Ai, Sj)} + + (1 – a)minj{V(Ai, Sj)} | maxi{a · maxj{V ´´ (Ai, Sj)} + (1 – a) × × minj{V(Ai, Sj)}} | ||
| S1 | S2 | S3 | |||||
| А1 | 2,5 | 3,5 | 4,0 | 4,0 | 2,5 | 4,0 · 0,6 + 2,5 · 0,4 = 3,4 | |
| А2 | 1,5 | 2,0 | 3,5 | 3,5 | 1,5 | 3,5 · 0,6 + 1,5 · 0,4 = 2,7 | |
| А3 | 3,0 | 8,0 | 2,5 | 8,0 | 2,5 | 8,0 · 0,6 + 2,5 · 0,4 = 5,8 | А3 |
| А4 | 7,5 | 1,5 | 3,5 | 7,5 | 1,5 | 7,5 · 0,6 + 1,5 · 0,4 = 5,1 |
Дата добавления: 2016-04-06; просмотров: 1586;
