Бета вклада ценной бумаги относительно оптимального портфеля
Оценим вклад каждой ценной бумаги, вошедшей в оптимальный портфель, в общую эффективность портфеля. Эффективность оптимального портфеля является случайной величиной, равной

(8.19)
где
R*=(R1 , R2, … Rn)- случайный вектор, составленный из случайных эффективностей
x+- структура оптимального портфеля ценных бумаг, равная согласно (8.9)
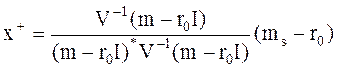
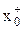 - количество средств, выделяемых на безрисковую ценную бумагу, для оптимального портфеля равное
- количество средств, выделяемых на безрисковую ценную бумагу, для оптимального портфеля равное 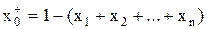 .
.
Таким образом, величины 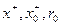 являются детерминированными, а величины
являются детерминированными, а величины 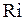 - случайными.
- случайными.
Тогда, математическое ожидание эффективности для оптимального портфеля равно
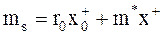
Отсюда разность между случайной эффективностью и средней эффективностью оптимального портфеля равна:
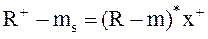 (8.20)
(8.20)
Вычислим величину 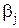 , именуемую «бета вклада j-ой ценной бумаги относительно оптимального портфеля». По определению она равна:
, именуемую «бета вклада j-ой ценной бумаги относительно оптимального портфеля». По определению она равна:
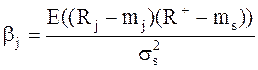 (8.21)
(8.21)
где 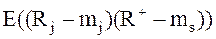 - ковариация эффективности j-ой ценной бумаги и эффективности оптимального портфеля.
- ковариация эффективности j-ой ценной бумаги и эффективности оптимального портфеля.
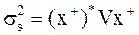 - дисперсия оптимального портфеля.
- дисперсия оптимального портфеля.
Коэффициенты βj – «бета вклад j-ой ценной бумаги относительно оптимального портфеля» называют также коэффициентами Шарпа.
С другой стороны, для βj можно дать следующее эквивалентное определение, частично проясняющее суть этой величины. Центрируем эффективность
j-ой ценной бумаги и эффективность оптимального портфеля, то есть от случайных величин Rj и R+ переходим к центрированным случайным величинам Rj - mj и R+ - ms.
Покажем, что βj является коэффициентом в линейной регрессии
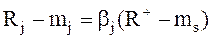 (8.22)
(8.22)
Действительно, найдем βj методом наименьших квадратов, то есть βj должен обеспечивать минимум дисперсии разности
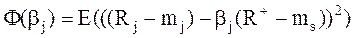 (8.23)
(8.23)
Раскрывая (8.23), получим для дисперсии
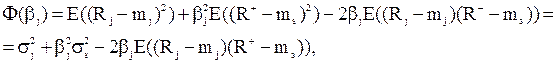 (8.24)
(8.24)
где σj2 – дисперсия (риск) j-ой ценной бумаги, σs2 – дисперсия (риск) оптимального портфеля,
E((Rj - mj)(R+ - ms)) – ковариация эффективности j-ой ценной бумаги и эффективности оптимального портфеля.
Приравняв производную от дисперсии (8.24) по βj нулю, получим линейное уравнение, которое дает выражение для βj в виде (8.21). Это и означает, что βj является коэффициентом в линейной регрессии.
Если вспомнить теперь, что ковариация связана с коэффициентом корреляции по формуле
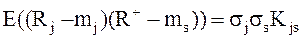 (8.25)
(8.25)
где σj –среднеквадратическое отклонение j-ой ценной бумаги, σs –среднеквадратическое отклонение оптимального портфеля, Kjs – коэффициент корреляции между эффективностью j-ой ценной бумаги и эффективностью портфеля ценных бумаг.
Тогда из (8.21) имеем:
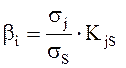 (8.26)
(8.26)
Таким образом, βj – «бета вклад j-ой ценной бумаги относительно оптимального портфеля» может с этой точки зрения рассматриваться как отношение среднеквадратических отклонений, умноженное на коэффициент корреляции.
Для выяснения экономического смысла рассмотрим βj с третьей точки зрения воспользуемся определением (8.21) и формулой (8.20). Вводя вектор столбец β, состоящий из всех коэффициентов β1, β2 … βn, получим из (8.21) и (8.20)
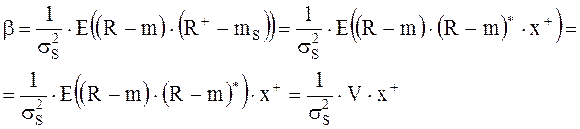
где V=E((R-m)(R-m)*) – ковариационная матрица размерности n×n для ценных бумаг (см. (8.3’), (6.6)).
Таким образом,
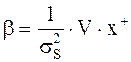 (8.27)
(8.27)
учитывая структуру оптимального портфеля
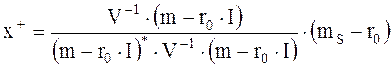
и структуру дисперсии оптимального портфеля
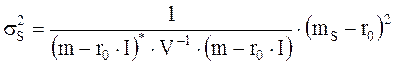
получим для β в матричном виде
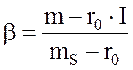 (8.28)
(8.28)
или
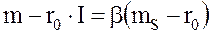
Окончательно в скалярной форме коэффициенты βj имеем:
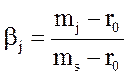 (8.29)
(8.29)
соответственно
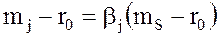 (8.30)
(8.30)
Отсюда следует важный вывод: премия за риск любой ценной бумаги, включенной в оптимальный портфель, пропорциональна премии за риск, связанный с оптимальным портфелем в целом, при этом коэффициент пропорциональности равен βj.
Пример 60.
Формирование портфеля из четырех ценных бумаг (задача J. Tobin).
Инвестор формирует портфель из четырех ценных бумаг, одна из которых является государственной безрисковой ценной бумагой. Средняя доходность портфеля m выражается формулой:
m = x0 + 5 x1 + 11 x2 + 21 x3, (8.30)
где: х0 – относительное количество средств потраченных на государственные безрисковые ценные бумаги;
х1, х2, х3 – относительное количество средств потраченных на три ценные бумаги с риском (акции).
При этом выполняется уравнение баланса:
х0 + х1 + х2 + х3 = 1 (8.31)
Риск портфеля определяется рискованными ценными бумагами и выражается формулой:
σ2 = х12+ 2 х22 + 5 х32 (8.32)
Необходимо определить структуру портфеля х0, х1, х2, х3 , обеспечивающую минимум риска (8.32) при выполнении условия баланса (8.31) и фиксации доходности (8.30).
Решение:
Вычитая из уравнения доходности (8.30) уравнение баланса (8.31), получим уравнение не содержащее переменной х0.
(x0+5x1+11x2+21x3)-( х0+х1+х2+х3)=m-1
4 x1 + 10 x2 + 20 x3 = m-1 (8.33)
Таким образом, задача упрощается. Нужно найти минимум функции риска (8.32) при одном ограничении (8.33).
Воспользовавшись функцией Лагранжа, получим:
L = х12+2 х22+5 х32 - λ (4 x1 + 10 x2 + 20 x3 - (m-1))
где λ – множитель Лагранжа.
Для достижения минимального значения вычислим и приравняем к нулю частные производные от функции Лагранжа:
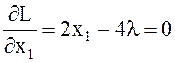
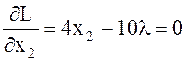
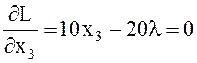
и в результате для х имеем:
x1 = 2λ, x2 = 2,5 λ, x3 = 2 λ (8.34)
Для вычисления множителя Лагранжа λ, подставим значения (8.34) в ограничения (8.33) и вычисляем значение множителя Лагранжа λ:
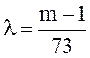
Подставляя значение λ в (8.34), вычисляем относительное количество средств потраченных на рискованные и государственные безрисковые ценные бумаги (значения х1,х2,х3,х0 ):
x1 = 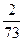 (m-1) = 0,02739(m-1)
(m-1) = 0,02739(m-1)
x2 = 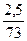 (m-1) = 0,03424(m-1) (8.35)
(m-1) = 0,03424(m-1) (8.35)
x3 = 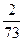 (m-1) = 0,02739(m-1)
(m-1) = 0,02739(m-1)
x0 =1 - 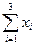 (m-1) =1- 0,08902(m-1)
(m-1) =1- 0,08902(m-1)
Для риска σ2 из (8.32) и (8.35) получим:
σ2 = х12+2х22+5х32= 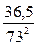 (m-1)2,
(m-1)2,
Следовательно, среднеквадратическое отклонение σ равно:
σ = 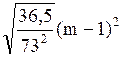 =
= 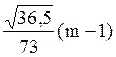 = 0,08276 (m-1)
= 0,08276 (m-1)
В качестве численного примера рассмотрим случай, когда желаемая доходность портфеля равна m=1, 2, 3, 11
| m | ||||
| x1 | 0,02739 | 0,05478 | 0,2739 | |
| x2 | 0,03424 | 0,06848 | 0,3424 | |
| x3 | 0,02739 | 0,05478 | 0,2739 | |
| x0 | 0,91098 | 0,82196 | 0,1098 | |
| σ | 0,08276 | 0,16552 | 0,8276 |
Таблица 8.1
Зависимость структуры портфеля и риска от доходности портфеля.
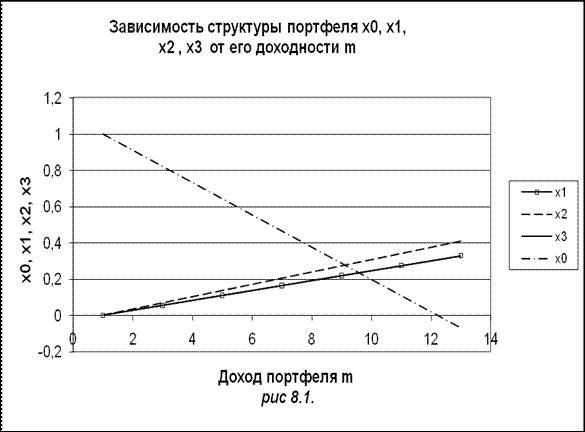
На рис.8.1. представлена зависимость структуры портфеля х0, х1, х2, х3 от доходности портфеля m. Прямые для х1 и х3 совпадают.
На рис.8.2. представлена зависимость риска портфеля σ от доходности портфеля m.

| |||||||||||
При доходности портфеля m = 1, равной доходности государственной ценной бумаги, получается очевидный результат х0=1, х1=0, х2=0, х3 =0,
т. е. все средства следует вложить в государственную ценную бумагу. При увеличении желаемой доходности портфеля средства начинают понемногу перетекать из государственной ценной бумаги в акции, причем пропорция между средствами на акции будет постоянной на первую и третью акцию одна и та же сумма на вторую акцию в 1,25 раз больше.
Таким образом, структура портфеля ценных бумаг не меняется в зависимости от желаемой доходности портфеля ценных бумаг. Пропорция: х1:х2:х3 не зависит от желаемой доходности портфеля ценных бумаг. Это свойство портфеля остается справедливым и в общем случае.
В общем случае задача оптимизации портфеля ценных бумаг решается численными методами, например, с помощью программы поиск решения из Excel. Для её подключения необходимо произвести следующие операции: войти в Excel, далее Сервис / Надстройки /Поиск решения.
На следующем модельном примере поясним суть понятия βj – вклада ценной бумаги (ЦБ) относительно оптимального портфеля.
Пример 61.
Расчет бета вклада ценной бумаги относительно оптимального портфеля.
В таблице 8.2 приведены эффективности R1, R2, R3 трех ценных бумаг (акций). Требуется найти статистические характеристики эффективностей акций необходимые для построения оптимального портфеля ценных бумаг, т. е. оценить математическое ожидание доходности акций m1, m2, m3; ковариационную vij и корреляционную kij матрицы связи ценных бумаг. Построить оптимальный портфель ценных бумаг (задача Д. Тобина) в предположении, что в него включена государственная ценная бумага с нулевым риском и ожидаемой доходностью r0 = 2. Рассчитать тремя способами (по формулам (8.21), (8.23), (8.29)) βj – вклада ценной бумаги относительно оптимального портфеля. Убедится в эквивалентности этих способов расчета βj – вклада ценной бумаги.
Таблица 8.2.
Эффективности ценных бумаг R1, R2, R3 и оптимального портфеля R+
| № | R1 | R2 | R3 | R+ |
| 8,761365 | 14,095503 | 23,632829 | 13,447617 | |
| 10,879587 | 10,690963 | 20,016460 | 12,389651 | |
| 8,257235 | 13,865662 | 21,150472 | 12,545236 | |
| 8,726669 | 12,580099 | 19,169947 | 11,859913 | |
| 8,552506 | 15,009649 | 22,962156 | 13,436746 | |
| 11,675297 | 16,566010 | 16,751497 | 13,399788 | |
| 9,413837 | 13,766254 | 16,835560 | 11,822925 | |
| 9,817628 | 15,297621 | 19,626172 | 13,115388 | |
| 11,913090 | 13,399956 | 21,672178 | 13,935806 | |
| 11,210324 | 16,575423 | 23,374822 | 14,964243 | |
| 9,504745 | 13,854966 | 21,109348 | 13,001792 | |
| 12,343175 | 11,811776 | 20,846186 | 13,457775 | |
| 8,384148 | 16,056675 | 23,868444 | 13,890185 | |
| 10,410748 | 11,591823 | 17,080349 | 11,683060 | |
| 12,111456 | 14,515588 | 18,742271 | 13,539585 | |
| 11,761857 | 14,033976 | 22,447792 | 14,251298 | |
| 9,634661 | 15,057955 | 23,045375 | 13,879325 | |
| 11,312833 | 16,998331 | 16,296277 | 13,259054 | |
| 7,753248 | 16,851225 | 17,937712 | 12,308721 | |
| 12,119974 | 10,701619 | 17,087648 | 12,091820 | |
| 11,917392 | 13,370214 | 19,974767 | 13,484292 | |
| 10,126544 | 11,554675 | 22,173056 | 12,901775 | |
| 7,815206 | 12,220851 | 18,212583 | 11,169482 | |
| 11,927865 | 11,978152 | 20,731739 | 13,315589 | |
| 8,453786 | 11,389094 | 22,542484 | 12,324045 | |
| 10,899179 | 16,787401 | 16,167041 | 13,013004 | |
| 9,990512 | 14,511945 | 17,875535 | 12,511885 |
Воспользовавшись программой СРЗНАЧ() в Excel, найдем ожидаемые доходности акций
m1= 10,21018, m2 = 13,89383, m3 = 20,04929
Далее, с помощью программ КОВАР() и КОРРЕЛ() найдем ковариационную и корреляционную матрицу соответственно.
Ковариационная матрица равна:
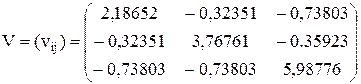
Корреляционная матрица равна:
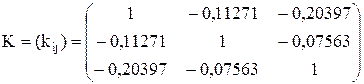
Коэффициенты корреляции малы и, следовательно, ценные бумаги статистически независимы.
Используя полученные значения ожидаемых доходностей портфеля m1, m2, m3 и ковариационную матрицу V, построим оптимальный портфель Д. Тобина с доходностью ms=13, включающий кроме акций государственную ценную бумагу с нулевым риском и доходом r0 = 2. Для этого воспользуемся программой Поиск решения в Excel. При вычислении риска портфеля x*V x, где х – вектор столбец средств вкладываемых в акции, можно использовать функцию Excel для умножения матриц МУМНОЖ().
Решение задачи Д. Тобина, в Excel дает следующую структуру оптимального портфеля ценных бумаг:
x0+ = 0,094160 , x1+ = 0,376906, x2+ = 0,266649, x3+ = 0262285,
где x0+ – доля средств выделяемых на покупку государственной ценной бумаги,
x1+, x2+, x3+ - доли средств выделяемых на покупку акций.
Эффективность оптимального портфеля является случайной величиной, равной согласно (8.19) равной

где
R* = (R1, R2, R3) - случайный вектор, составленный из случайных эффективностей трех акций,
Х0+, Х+ = (Х1+ , Х2+ , Х3+) - вычисленная структура оптимального портфеля ценных бумаг.
В таблице 8.2. столбец R+ соответствует оптимальному портфелю.
Вычислим величину 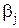 , именуемую «бета вклада j-ой ценной бумаги относительно оптимального портфеля» по формуле (8.21):
, именуемую «бета вклада j-ой ценной бумаги относительно оптимального портфеля» по формуле (8.21):
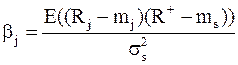
где 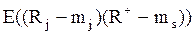 - ковариация эффективности j-ой ценной бумаги и эффективности оптимального портфеля.
- ковариация эффективности j-ой ценной бумаги и эффективности оптимального портфеля.
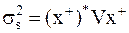 - дисперсия оптимального портфеля.
- дисперсия оптимального портфеля.
Коэффициенты βj – «бета вклад j-ой ценной бумаги относительно оптимального портфеля» называют также коэффициентами Шарпа.
Вычислив ковариации между парами столбцов (R1, R+), (R2, R+), (R3, R+) в таблице 8.2. и поделив её на дисперсию оптимального портфеля, получим бета вклада j-ой ценной бумаги относительно оптимального портфеля:
β1 = 0,7464, β2 = 1,0810, β3 = 1,6408.
С другой стороны, для βj можно дать следующее эквивалентное определение: βj - является коэффициентом в линейной регрессии:
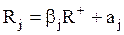 (8.36)
(8.36)
Найдем параметры линейной регрессии βj и аj методом наименьших квадратов (8.23), используя в Excel функцию ЛИНЕЙН() для построения линейной регрессии между столбцами R1, R2, R3, и R+. Получим соответственно:
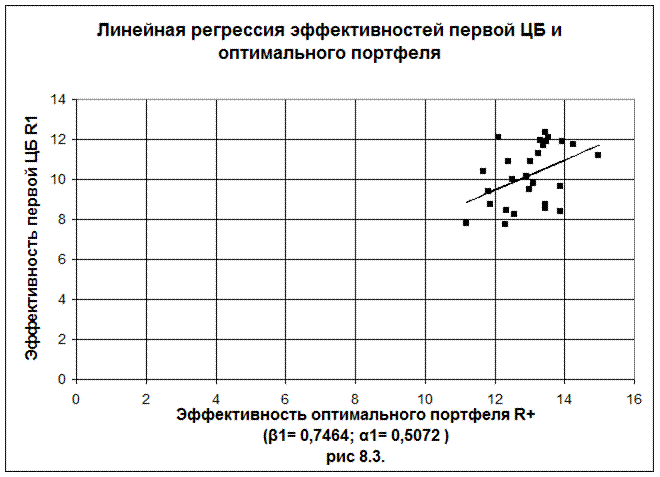
β1 = 0,7464, a1 = 0,5072
β2 = 1,0810, a2 = - 0,1625
β3 = 1,6408 a3 = - 1,2817
На рисунках 8.3. - 8.5. проиллюстрирована линейная регрессия пар эффективностей ценных бумаг и эффективности оптимального портфеля.
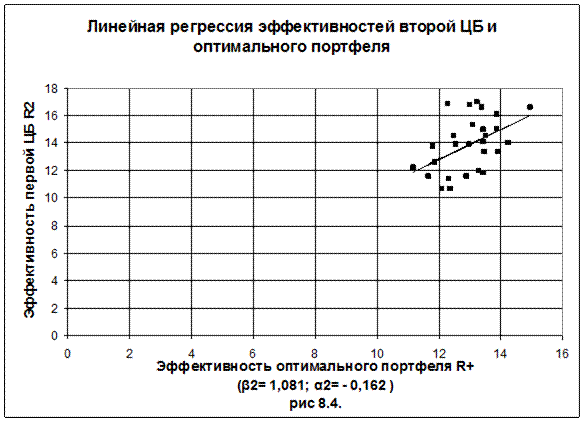
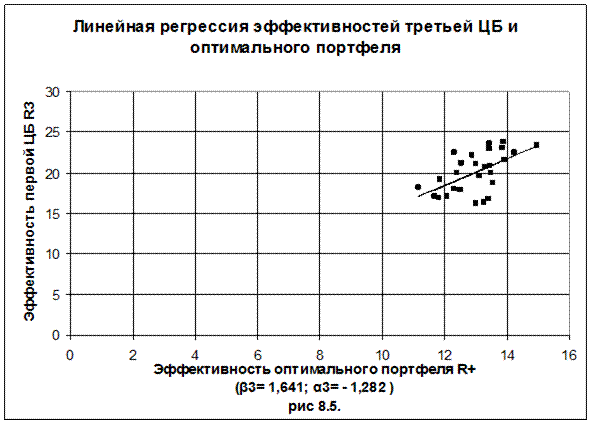
С третьей точки зрения экономический смысл βj следующий. Коэффициент βj равен отношению разности доходности акции и государственной ценной бумаги к разности доходности оптимального портфеля и государственной ценной бумаги (см. формулу 8.29):
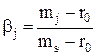
или (см. формулу (8.30)):
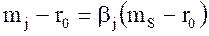
Таким образом, премия за риск любой ценной бумаги, включенной в оптимальный портфель, пропорциональна премии за риск, связанный с оптимальным портфелем в целом, при этом коэффициент пропорциональности равен βj.
Расчет по формуле (8.29) дает следующие значения для βj – вклада ценной бумаги
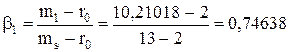
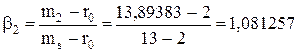
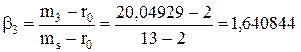
Очевидно, что во всех трех случаях расчета βj – вклада ценной бумаги получаются одинаковые значения.
В соответствии с моделью ценообразования на рынке капиталовложений (Capital Asset Pricing Model, CAPM), разработанной Шарпом, Линтнер и Моссин формулы (8.29) и (8.30) применимы для конкурентного равновесного финансового рынка. Для этого нужно заменить индекс оптимального портфеля ms на индекс рынка, и тогда формула (8.30):
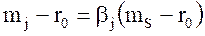 (8.37)
(8.37)
означает следующее: премия за риск, связанный с любой ценной бумагой 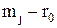 , пропорциональна премии за риск рынка в целом
, пропорциональна премии за риск рынка в целом 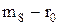 , а коэффициент пропорциональности есть βj - бета вклада ценной бумаги относительно рынка.
, а коэффициент пропорциональности есть βj - бета вклада ценной бумаги относительно рынка.
Соотношение (8.31) принято называть основным уравнением равновесного рынка. Его графическое изображение представлено на рис 8.6.
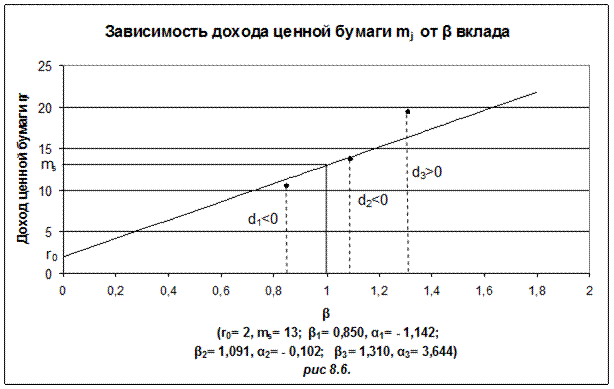
По оси абсцисс отложена величина бета, по оси ординат ожидаемая доходность ценной бумаги. Для идеального равновесного рынка задание бета позволяет найти ожидаемую эффективность в виде точки на прямой.
Поведение реального стационарного рынка вносит в формулу (8.37) статистическую погрешность αj и формула приобретает вид:
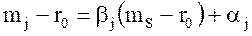 , (8.38)
, (8.38)
Она отличается от основного уравнения САРМ (8.38) наличием слагаемого (погрешности), называемой альфа вклада.
Если с помощью линейной регрессии 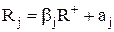 определены параметры бета вклада и величины
определены параметры бета вклада и величины 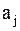 , то альфа вклада определяется по формуле:
, то альфа вклада определяется по формуле:
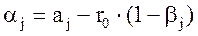
Для идеального рынка альфа вклады всех ценных бумаг равны нулю. Статистические данные реального стационарного рынка говорят о наличии погрешности в модели САРМ, которые приводят к появлению заметных альфа вкладов.
Объясняется это тем, что на реальном рынке отнюдь не все участники одинаково информированы, и рациональность их поступков различна. Поэтому портфель рынка отличается от оптимального портфеля.
Тогда, если статистика показывает, что альфа вклада какой-нибудь бумаги αj > 0 положительна, то это означает недооценку рынком этой ценной бумаги. В противном случае при αj < 0 считают, что рынок переоценивает возможности этой бумаги. В первом случае при αj > 0 следует играть на повышении курс ценной бумаги, во втором случае при αj < 0 на понижении курса.
В приведенном на рис 8.6. примере реального «возмущенного» рынка бета и альфа равны:
Таблица 8.3.
| β1 | 0,85043 | α1 | -1,14257 |
| β2 | 1,09073 | α2 | -0,10161 |
| β3 | 1,30983 | α3 | 3,64429 |
Бета вклада ценной бумаги реального рынка немного отличаются от бета вклада ценной бумаги идеального рынка, рассмотренного выше, и альфа неравны нулю и отличие от идеального рынка, где они равны нулю.
Первая ценная бумага дает доход ниже рынка β1<1 и недооценена α1<0.
Вторая ценная бумага дает доход выше рынка β2>1 и недооценена α2<0.
Третья ценная бумага дает доход выше рынка β3>1 и переоценена α3>0.
Дата добавления: 2016-03-15; просмотров: 1838;
