Полное решение задачи Марковица для трех ценных бумаг.

Рассмотрим полное численное решение задачи Марковица (H.Markowitz) для трех ценных бумаг. Портфель состоит из трех независимых ценных бумаг и будет описываться следующими уравнениями:

x₁ + x₂ + x₃ = 1 (7.25)

m_s = 10 x₁ +20 x₂ +40 x₃ (7.26)

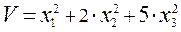(7.27)

Ковариационная матрица в этом случае будет равна:

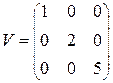
Поиск оптимального портфеля ценных бумаг производиться методом Лагранжа. Функция Лагранжа будет равна:

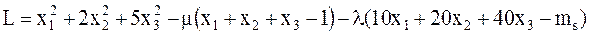
где µ, λ - множители Лагранжа. Вычислим частные производные:

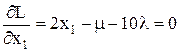
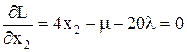
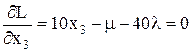
Отсюда:

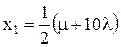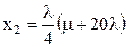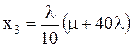, , (7.28)

Подставляя структуру портфеля (7.28) в линейные ограничения (7.25) и (7.26) получим систему из двух линейных уравнений с двумя неизвестными множителями Лагранжа µ и λ

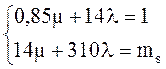(7.29)

Решаем систему методом Крамера, при этом определители будут равны:

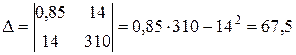
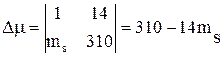
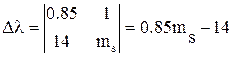
Окончательно для множителя Лагранжа получим:

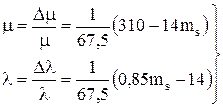(7.30)

Подставляя (7.30) в (7.28) получим структуру портфеля:

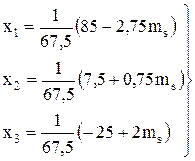(7.31)

Подставляя значения х (7.31) в формулу (7.27) для риска получим:

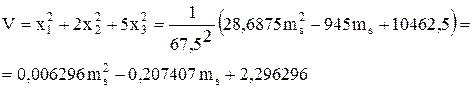(7.32)

Риск портфеля достигает минимума при m_s = 945/(2 28,6875)=16,4706 V_min=0,58824. Это соответствует оптимальному решению задачи об осторожном инвесторе (см. пример 58, рис 7.2.).

Из формулы (7.30) видно, что структура портфеля: х₁, х₂, х₃, – относительное количество средств, вкладываемых в ценные бумаги, линейно зависит от заданной доходности портфеля m_s (см. рис.7.1.). С ростом доходности портфеля m_s уменьшается количество средств вкладываемых в первую бумагу х₁, и возрастает количество средств вкладываемых во вторую и третью бумагу х₂, х₃.

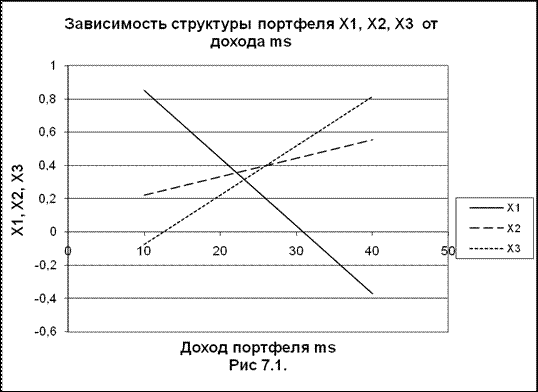
Риск портфеля ценных бумаг является квадратичной функцией от задаваемого дохода m_s (см. рис.7.2.).

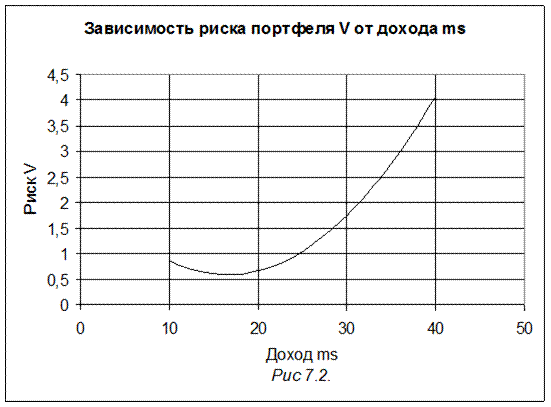
График зависимости риска портфеля от суммарного дохода портфеля является параболой с минимумом в точке (16,47; 0,588) т.е. при доходе 16,47 риск равен 0,588 , что соответствует оптимальному решению задачи об осторожном инвесторе (см. пример 58).

В общем случае задача оптимизации портфеля ценных бумаг решается численными методами, например, с помощью программы поиск решения из Excel. Для её подключения необходимо произвести следующие операции: войти в Excel, далее Сервис / Надстройки /Поиск решения.