Оценка доходности и риска портфеля ценных бумаг

Предположим, что портфель инвестора содержит n ценных бумаг с эффективностями R₁, R₂, ¼, R_n. На приобретение ценных бумаг истрачена сумма, которую удобно принять за единицу. Пусть x₁, x₂, ¼, x_n – суммы, потраченные на приобретение 1, 2, ¼, n-ой бумаги. Тогда:

х₁+х₂+¼+х_n=1 или 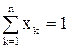. (6.1)

Эффективность портфеля будет равна:

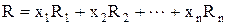или . (6.2)

Используя свойства линейности математического ожидания, для ожидаемой (средней) эффективности портфеля m получим:

,

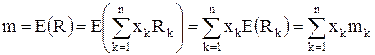или окончательно:

. (6.3)

Отклонение эффективности портфеля R от ожидаемой эффективности равно:

.

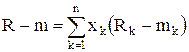Математическое ожидание квадрата отклонения (R-m)² является дисперсией (вариацией). Оно определяет меру риска для портфеля и равно в силу линейности математического ожидания величине:

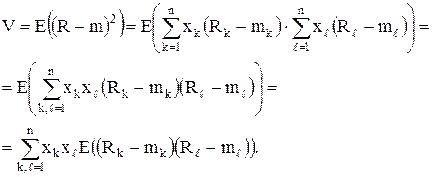
Окончательно:

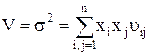, (6.4)

где – ковариация случайных величин R_i и R_j.

Она связана с коэффициентами корреляции k_ij случайных величин R_i и R_j формулой:

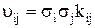, (6.5)

где

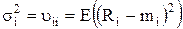– дисперсия R_i;

– дисперсия R_j.

Таким образом, риск портфеля инвестора определяется дисперсией, являющейся квадратичной формой относительно x₁, x₂, ¼, x_n и заданной симметричной матрицей:

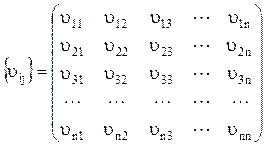(6.6)

где .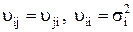

В развернутом виде (6.4) запишется:

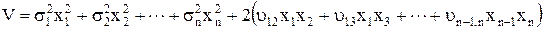. (6.7)

Выпишем основные уравнения, характеризующие портфель:

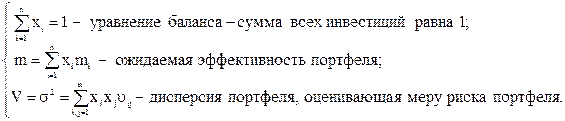(6.8)

Далее рассмотрим частные случаи.