Портфель из антикоррелированных ценных бумаг
Рассмотрим упрощенный модельный случай, отражающий, впрочем, суть проблемы. Пусть портфель инвестора состоит из двух ценных бумаг, находящихся в состоянии обратной корреляции (или антикорреляции). Тогда, коэффициент корреляции между эффективностями 1-ой и 2-ой ценной бумагой равен
-1: 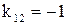 . Отсюда, дисперсия, оценивающая риск портфеля, равна:
. Отсюда, дисперсия, оценивающая риск портфеля, равна:
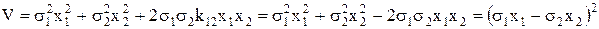 .
.
Очевидно, если деньги инвестора разделены в пропорции 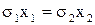 , то риск портфеля равен нулю.
, то риск портфеля равен нулю.
Учитывая, что х1+х2=1, получим:
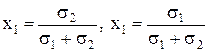 .
.
Эффективность портфеля равна:
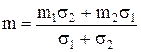
и будет лежать в пределах от min (m1, m2) до mах (m1, m2).
Таким образом, при наличии антикорреляции возможен портфель инвестора с нулевым риском.
7. ОПТИМАЛЬНЫЙ ПОРТФЕЛЬ ПРИ РИСКОВАННЫХ ВЛОЖЕНИЯХ
(H. MARKOWITZ)
Можно составить две задачи оптимизации портфеля:
1. распределить средства, выделяемые на покупку ценных бумаг так, чтобы при фиксированной эффективности обеспечить минимальный риск;
2. распределить средства, выделяемые на покупку ценных бумаг так, чтобы при фиксированном риске обеспечить максимальное значение эффективности.
Математическая постановка задач следующая.
Задача 1.
Минимизация риска.
Найти структуру портфеля ценных бумаг x1, x2, ¼, xn, удовлетворяющие линейным ограничениям:
x1+x2+¼+xn=1 (уравнение баланса); (7.1)
x1m1+x2m2+¼+xnmn=ms (фиксация эффективности) (7.2)
и минимизирующие квадратичную функцию риска
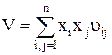 . (7.3)
. (7.3)
Задача 2.
Максимизация эффективности.
Найти структуру портфеля ценных бумаг x1, x2, ¼, xn, удовлетворяющие линейному ограничению:
x1+x2+¼+xn=1 (уравнение баланса); (7.1¢)
и квадратичному ограничению:
 (фиксация риска) (7.2¢)
(фиксация риска) (7.2¢)
и максимизирующие линейную функцию дохода:
m=x1m1+x2m2+¼+xnmn (7.3¢)
Приведенные задачи двойственны и приводят к одному и тому же решению.
Решение этих задач может содержать некоторые значения xk<0. Это означает, что при формировании оптимального портфеля для покупки k-ой ценной бумаги следует взять в долг сумму – xk. Если портфель ценных бумаг уже существует, то следует продать пакет из к-ых ценных на сумму – xk.
Если в долг брать нельзя, то дополнительно к ограничениям равенствам в задаче оптимизации добавляются ограничения неравенства:
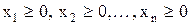 . (7.4)
. (7.4)
Рассмотрим сначала задачу построения оптимального портфеля инвестора без ограничения неотрицательности переменных.
Если в задаче оптимизации портфеля на переменные не наложено условие неотрицательности, то задача имеет точное аналитическое решение.
Воспользуемся функцией Лагранжа.
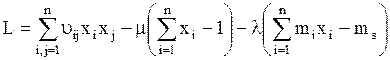 , (7.5)
, (7.5)
где
ms – требуемое значение эффективности портфеля;
l, m – множители Лагранжа, которые будут найдены позже из линейных ограничений.
Приравнивая частные производные 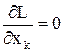 , получим систему линейных уравнений для определения x1, x2, ¼, xn:
, получим систему линейных уравнений для определения x1, x2, ¼, xn:
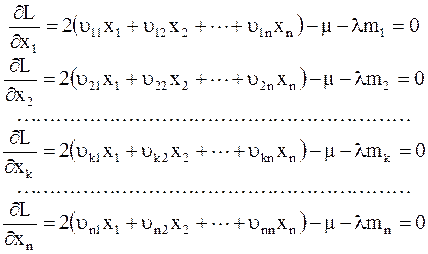 (7.6)
(7.6)
Далее удобно использовать матричные обозначения. Тогда (7.6) можно записать в виде:
2Vx=mI+lm, (7.7)
где V – симметричная знакоположительная матрица ковариации размерности n´n, равная:
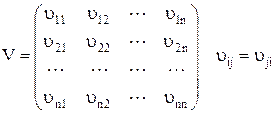 ,
,
x – вектор-столбец неизвестных n´1
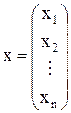
I, m – векторы-столбцы n´1 вида
 .
.
Воспользовавшись обратной матрицей V–1, получим для вектора-столбца неизвестных формулу:
 . (7.8)
. (7.8)
Осталось определить множители Лагранжа из линейных ограничений, записываемых в матричном виде:
I*x=1, m*x=ms, (7.9)
где
m*, I* – векторы строки, получаемые из векторов-столбцов с помощью операции транспортирования, обозначаемой *.
Подставляя (7.8) в (7.9), получим систему линейных уравнений для определения m, l:
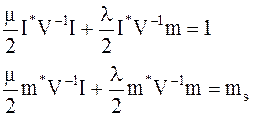 (7.10)
(7.10)
Вводя обозначения: 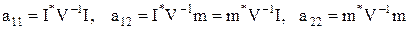 , получим:
, получим:
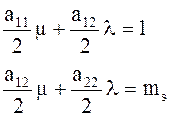 (7.11)
(7.11)
Решая методом Крамера систему (7.11), получим:

Подставляя в (7.8) найденные множители Лагранжа, получим оптимальную структуру портфеля в виде:
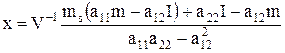 . (7.12)
. (7.12)
Из (7.12) видно, что х линейно зависит от требуемой доходности портфеля ms (см. рис. 7.1.). Тогда риск, равный 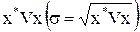 будет квадратичной выпуклой вниз функцией от требуемой доходности портфеля ms (см. рис. 7.2.).
будет квадратичной выпуклой вниз функцией от требуемой доходности портфеля ms (см. рис. 7.2.).
Рассмотрим теперь задачу минимизации функции риска с дополнительными ограничениями (условия неотрицательности неизвестных) в виде неравенств (7.4). Дадим геометрическую интерпретацию решения этой задачи.
Функции риска является квадратичной формой неизвестных. Два линейных ограничения 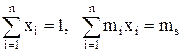 выделяют в n-мерном пространстве неизвестных подпространство n–2-мерной размерности, соответствующее независимым переменным. В этом подпространстве n неравенств (xi³0) ограничивает некоторый выпуклый многогранник размерности n–2. Минимизируемая функция является квадратичной знакоположительной, поэтому минимум может достигаться как внутри многогранника, так и на его границе.
выделяют в n-мерном пространстве неизвестных подпространство n–2-мерной размерности, соответствующее независимым переменным. В этом подпространстве n неравенств (xi³0) ограничивает некоторый выпуклый многогранник размерности n–2. Минимизируемая функция является квадратичной знакоположительной, поэтому минимум может достигаться как внутри многогранника, так и на его границе.
Данная задача относится к проблеме квадратичного программирования, для решения которой разработаны специальные численные методы.
Эта задача может быть решена с использованием универсальных математических программных средств, например, Excel, Mathcad, Matlab, Maple или специальных программных средств, применяющих метод проекции градиента (Розена) и имеющихся в СЗАГС.
Пример58.
Задача об осторожном инвесторе.
В качестве численного примера рассмотрим решение задачи для случая трех ценных бумаг: Портфель состоит из 3-х независимых ценных бумаг, и описываться следующими уравнениями:
x1 + x2+ x3 = 1 (уравнение баланса); (7.13)
m = 10∙x1 +20∙x2 +40∙x3 (уравнение дохода) (7. 14)
При этом риск портфеля будет равен:
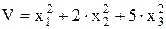 (уравнение риска) (7. 15)
(уравнение риска) (7. 15)
Следует найти структуру портфеля ценных бумаг, обеспечивающую минимальный риск (7.15) при выполнении линейного ограничения уравнения баланса (7.13). Определить доходность и риск оптимального портфеля осторожного инвестора.
В этом случае осторожный инвестор минимизирует риск, а доход, какой уж получится. Поиск оптимального портфеля ценных бумаг производится методом Лагранжа. Функция Лагранжа будет равна:
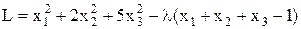 ,
,
где λ - множитель Лагранжа.
Вычислим частные производные:
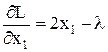 ,
, 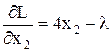 ,
, 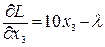
Отсюда, приравнивая к нулю производные, получим структуру портфеля ценных бумаг:
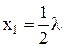 ,
, 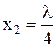 ,
, 
Уже на этом этапе решения задачи очевидна структура портфеля. Если в первую ценную бумагу вложено 100 тыс. руб., то во вторую и третью нужно вложить в два и пять раз меньше средств, соответственно, 50 и 20 тыс. руб.
Найдем количество средств, вкладываемых в ценные бумаги в относительных единицах. Для этого определим множителя Лагранжа λ, воспользовавшись уравнением баланса (7. 13):
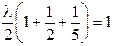
Окончательно имеем:
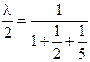
Тогда структура портфеля приобретет вид:
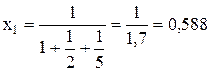
 (7.16)
(7.16)

Подставим значения x в уравнения (7. 14) и (7. 15), и найдем значения дохода и риска оптимального портфеля:
m=10∙0,588+20∙0,294+40∙0,118 = 16,4705
V = 0,5882 + 2∙ 0,2942 + 5∙0,1182 = 0,588
Представим полученные результаты в виде таблицы 7.1. Первая строка соответствует оптимальному портфелю осторожного инвестора. Вторая, третья и четвертая строки предполагает вложение всех средств в первую, вторую и третью ценную бумагу соответственно
Таблица 7.1.
| x1 | x2 | x3 | m | V |
| 0,588 | 0,924 | 0,118 | 16,48 | 0,588 |
На первый взгляд, кажется, что минимальный риск достигается в случае, когда все средства вкладывать в наименее рискованную первую ценную бумагу. При этом доходность достигает 10, а риск достигает 1. Однако в случае оптимальной диверсификации портфеля следует вложить 58,8 % в первую ценную бумагу, во вторую 29,4 % и в третью 11,8 %. При этом оказывается, что доход портфеля возрастет более чем в 1,648 раза и будет равен 16,48, а риск уменьшиться почти в два раза и будет равен 0,588.
Дата добавления: 2016-03-15; просмотров: 1062;
