Неравенство Чебышева

Для оценки рискованности операции и выбора средств ограничения риска может быть полезна теорема Чебышева для случайных величин. В простейшем случае она связывает меру отклонения случайной величины R от ее математического ожидания m с ее дисперсией s². Точнее она формулируется так.

Теорема Чебышева

Вероятность того, что случайная величина R отклонится от своего математического ожидания m больше, чем заданное значение d, не превосходит ее дисперсии s², деленной на d², т. е.:

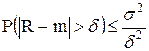, (5.4)

где Р(*) обозначает вероятность события *.

Воспользуемся теоремой Чебышева для решения следующей задачи.

Пример 57.

Господин А делает заем под процент r и под залог недвижимости. На полученные взаймы деньги господин А покупает акции. Какова вероятность того, что господин А не сможет вернуть долг и лишится недвижимости?

Решение.

Будем считать, что эффективность R покупаемых господином А акций характеризуется математическим ожиданием доходности m и дисперсией s². Отметим, что сделка имеет смысл, если m>r. Однако вероятность разорения все равно остается. Событие, которое приводит к разорению инвестора, состоит в следующем:

R<r, (5.5)

т. е. эффективность вложения в акции R меньше r процентной ставки займа. Здесь R – случайная величина, а r – детерминированная величина. Из (5.5) следует 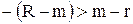. Тогда, для вероятности имеем:

.

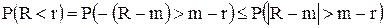Далее воспользуемся неравенством Чебышева (5.4):

.

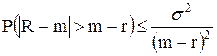Окончательно, для вероятности разорения инвестора имеем неравенство:

.

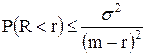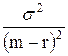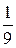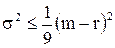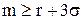Таким образом, вероятность разориться не превосходит величины . Если инвестор хочет, чтобы шанс разориться не превышал , то достаточно выполнения условия: или , т. е. ожидаемая эффективность вложения в акции должна быть больше процентной ставки займа плюс три среднеквадратических отклонения 3s. При этом вероятность разорения будет менее .

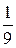Хеджирование

Хеджирование (hedging) – любая схема, позволяющая исключить или ограничить риск финансовых операций, связанных с ценными бумагами.

Для иллюстрации хеджирования рассмотрим следующий модельный пример.

Инвестор-кредитор А собирается вложить сумму С в дело под r процентов. Ожидаемый доход равен R=Cr. Однако операция инвестору представляется рискованной, и он решает приобрести страховой полис, гарантирующий выплату определенной суммы в случае провала сделки.

Для этого сумму С инвестор разделяет на две части: Cx он вкладывает в сделку и, C(1-x) он тратит на страховку, где х, 1-х – доля суммы, потраченная на финансовую сделку и страховой полис соответственно. Возможны два варианта развития событий.

Вариант 1.

Сделка оказалась удачной. В результате получен доход:

.

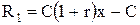Вариант 2.

Сделка не удалась. Инвестор получает страховую выплату в размере 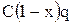, где q – отношение страхового возмещения к цене полиса. Тогда полученный доход равен:

.

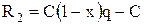Очевидно, логично выбрать х так, чтобы доход в обоих случаях был одинаков R₁=R₂. Решив линейное уравнение, получим:

.

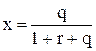При этом доход будет равен:

.

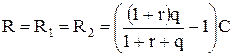Таким образом, данная схема хеджирования исключает неопределенность, при этом эффективность сделки снижается с r до .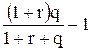

Рассмотрим численный пример. Пусть r=20 % = 0,2, а q = 50. Тогда доля средств, отпускаемых на сделку, будет равна: .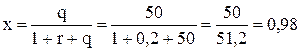

Доля средств на страховку будет равна 1–х=0,02. Эффективность уменьшается с r=20 % до .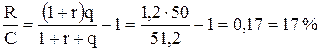

Таким образом, за счет небольшого уменьшения эффективности с 20 % до 17 % удастся уменьшить финансовый риск сделки.